用局部加权回归散点平滑法观察二维变量之间的关系

二维变量之间的关系研究是很多统计方法的基础，例如回归分析通常会从一元回归讲起，然后再扩展到多元情况。局部加权回归散点平滑法（locally weighted scatterplot smoothing，LOWESS或LOESS）是查看二维变量之间关系的一种有力工具。

LOWESS主要思想是取一定比例的局部数据，在这部分子集中拟合多项式回归曲线，这样我们便可以观察到数据在局部展现出来的规律和趋势；而通常的回归分析往往是根据全体数据建模，这样可以描述整体趋势，但现实生活中规律不总是（或者很少是）教科书上告诉我们的一条直线。我们将局部范围从左往右依次推进，最终一条连续的曲线就被计算出来了。显然，曲线的光滑程度与我们选取数据比例有关：比例越少，拟合越不光滑（因为过于看重局部性质），反之越光滑。

本文的数据文件：物种数目与海拔高度（感谢中科院植物所赖江山博士提供数据并授权使用）

R程序代码：

# 从本站counts.txt文件直接将数据读入R
x = read.csv("https://cos.name/wp-content/uploads/2008/11/counts.txt")
par(las = 1, mar = c(4, 4, 0.1, 0.1))
plot(x, pch = 20, col = rgb(0, 0, 0, 0.5))
# 取不同的f参数值
for (i in seq(0.01, 1, length = 100)) {
    lines(lowess(x$altitude, x$counts, f = i), col = gray(i),
        lwd = 1.5)
    Sys.sleep(0.15)
}

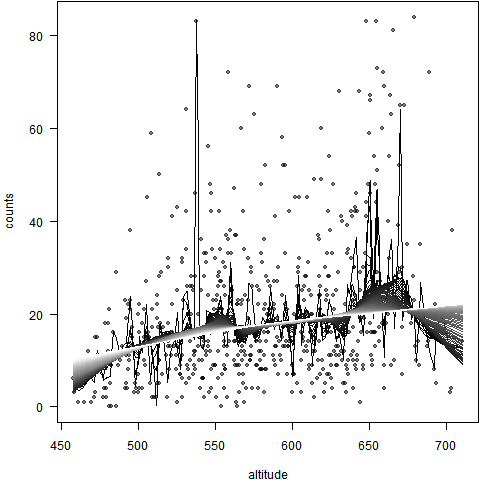
以上Sys.sleep()语句只是为了让读者看清楚添加LOWESS曲线的过程，实际画图过程中可以去掉。以上代码生成的图形如下：

上图中，曲线颜色越浅表示所取数据比例越大。不难看出白色的曲线几乎已呈直线状，而黑色的线则波动较大。总体看来，图中大致有四处海拔上的物种数目偏离回归直线较严重：450米、550米、650米和700米附近。若研究者的问题是，多高海拔处的物种数最多？那么答案应该是在650米附近。如果仅仅从回归直线来看，似乎是海拔越高，则物种数目越多。如此推断下去，恐怕月球或火星上该物种最多。以下是回归直线的图示：

par(las = 1, mar = c(4, 4, 0.1, 0.1), mgp = c(2.5,
    1, 0))
plot(x, pch = 20, col = rgb(0, 0, 0, 0.5))
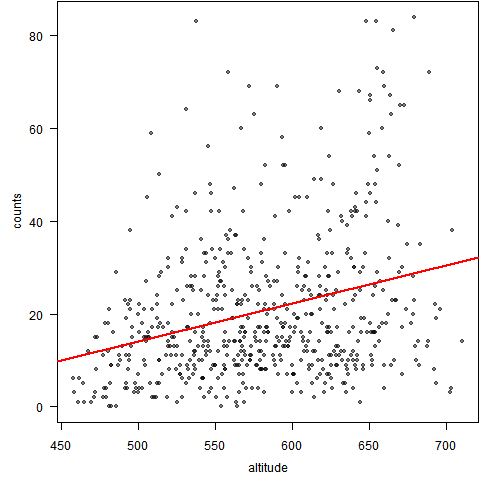
abline(lm(counts ~ altitude, x), lwd = 2, col = "red")

为了确保我们用LOWESS方法得到的趋势是稳定的，我们可以进一步用Bootstrap的方法验证。因为Bootstrap方法是对原样本进行重抽样，根据抽得的不同样本可以得到不同的LOWESS曲线，最后我们把所有的曲线添加到图中，看所取样本不同是否会使得LOWESS有显著变化；以下是R代码：

set.seed(711) # 设定随机数种子，保证本图形可以重制
par(las = 1, mar = c(4, 4, 0.1, 0.1), mgp = c(2.5,
    1, 0))
plot(x, pch = 20, col = rgb(0, 0, 0, 0.5))
for (i in 1:400) {
    idx = sample(nrow(x), 300, TRUE) # 有放回抽取300个样本序号
    lines(lowess(x$altitude[idx], x$counts[idx]), col = rgb(0,
        0, 0, 0.05), lwd = 1.5) # 用半透明颜色，避免线条重叠使得图形看不清
    Sys.sleep(0.05)
}
dev.off()

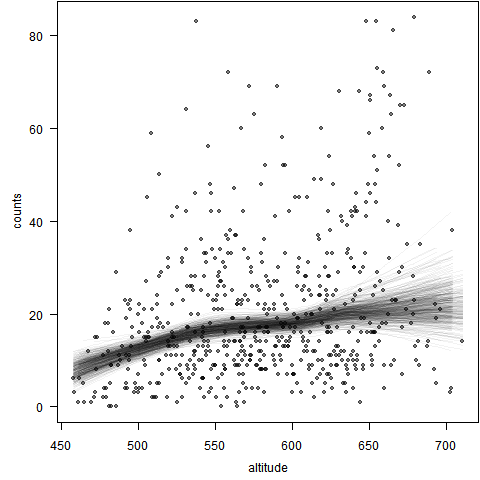
生成图形如下：

可以看出，经过400次重抽样并计算LOWESS曲线，刚才在第一幅图中观察到的趋势大致都还存在（因为默认取数据比例为2/3，因此拟合曲线都比较光滑），只是700米海拔附近物种数目减小的趋势并不明显了，这是因为这个海拔附近的观测样本量较少，在重抽样的时候不容易被抽到，因此在图中代表性不足，最后得到的拟合曲线分布稀疏。

作者注：只是一副散点图而已，能做的文章并不少。本文是基于赖博士的另外一个问题而引发出来的思考，供生物与生态专业的同仁参考。值此新建站点之际，谨以此文抛砖，望能引来更多高人对COS网站贡献的“美玉”。作者联系方式：xie[at]yihui.name