跑完分类模型(Logistic 回归、决策树、神经网络等),我们经常面对一大堆模型评估的报表和指标,如 Confusion Matrix、ROC、Lift、Gini、K-S 之类(这个单子可以列很长),往往让很多在业务中需要解释它们的朋友头大:“这个模型的 Lift 是 4,表明模型运作良好。——啊,怎么还要解释 ROC,ROC 如何如何,表明模型表现良好……” 如果不明白这些评估指标的背后的直觉,就很可能陷入这样的机械解释中,不敢多说一句,就怕哪里说错。本文就试图用一个统一的例子(SAS Logistic 回归),从实际应用而不是理论研究的角度,对以上提到的各个评估指标逐一点评,并力图表明:
- 这些评估指标,都是可以用白话(plain English, 普通话)解释清楚的;
- 它们是可以手算出来的,看到各种软件包输出结果,并不是一个无法探究的 “黑箱”;
- 它们是相关的。你了解一个,就很容易了解另外一个。
本文从混淆矩阵 (Confusion Matrix,或分类矩阵,Classification Matrix) 开始,它最简单,而且是大多数指标的基础。
数据
本文使用一个在信用评分领域非常有名的免费数据集,German Credit Dataset,你可以在 UCI Machine Learning Repository 找到(下载;数据描述。另外,你还可以在 SAS 系统的 Enterprise Miner 的演示数据集中找到该数据的一个版本(dmagecr.sas7bdat)。以下把这个数据分为两部分,训练数据 train 和验证数据 valid,所有的评估指标都是在 valid 数据中计算(纯粹为了演示评估指标,在 train 数据里计算也未尝不可),我们感兴趣的二分变量是 good_bad,取值为 {good, bad}:
Train data
good_bad Frequency Percent
-------------------------------------------
bad 154 25.67
good 446 74.33
Valid data
good_bad Frequency Percent
--------------------------------------------
bad 146 36.50
good 254 63.50
信用评分指帮助贷款机构发放消费信贷的一整套决策模型及其支持技术。一般地,信用评分技术将客户分为好客户与坏客户两类,比如说,好客户 (good) 能够按期还本付息(履约),违约的就是坏客户(bad)。具体做法是根据历史上每个类别(履约、违约)的若干样本,从已知的数据中考察借款人的哪些特征对其拖欠或违约行为有影响,从而测量借款人的违约风险,为信贷决策提供依据。Logistic 回归是信用评分领域运用最成熟最广泛的统计技术。
约定
在我们的示例数据中,要考察的二分变量是 good_bad,我们把感兴趣的那个取值 bad(我们想计算违约的概率),称作正例 (Positive, 1),另外那个取值 (good)称作负例 (Negative, 0)。在 SAS 的 Logistic 回归中,默认按二分类取值的升序排列取第一个为 positive,所以默认的就是求 bad 的概率。(若需要求 good 的概率,需要特别指定)。
模型
如果没有特别说明,以下所有的 SAS 代码都在 SAS 9.1.3 SP4 系统中调试并运行成功(在生成 ROC 曲线时,我还会提到 SAS9.2 的新功能)。
proc logistic data=train;
model good_bad=checking history duration savings property;
run;
这个数据很整齐,能做出很漂亮的模型,以下就直接贴出参数估计的结果:
Analysis of Maximum Likelihood Estimates
Standard Wald
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 0.6032 0.4466 1.8242 0.1768
checking 1 -0.6536 0.0931 49.3333 <.0001
history 1 -0.4083 0.0980 17.3597 <.0001
duration 1 0.0248 0.00907 7.4820 0.0062
savings 1 -0.2017 0.0745 7.3308 0.0068
property 1 0.3157 0.1052 9.0163 0.0027
回归方程就是:
logit[p(bad)]=log(p/1-p)
=0.6032-0.6536*checking-0.4083*history+0.0248*duration
-0.2017*savings+0.3157*property
用下面的公式就可以求出正例的概率(bad 的概率):
上式求出的是概率值,如何根据概率值把各个客户归类,还需要一个阈值,比如,这里我们简单地规定,违约概率超过 0.5 的就归为 bad,其余为 good。把上述公式代入 valid 数据中,
data valid_p;
set valid;
logit=0.6032-0.6536*checking-0.4083*history+0.0248*duration-0.2017*savings+0.3157*property;
p=exp(logit)/(exp(logit)+1);
if p<0.5 then good_bad_predicted='good';
else good_bad_predicted='bad';
keep good_bad p good_bad_predicted;
run;
从下面的局部的数据 valid_p 可以看到,一些实际上是 good 的客户,根据我们的模型(阈值 p 取 0.5),却预测他为 bad(套用我们假设检验的黑话,这就犯了 “弃真” 的错误),对一些原本是 bad 的客户,却预测他为 good(“取伪” 错误),当然,对更多的客户,good 还预测成 good,bad 还预测成 bad:
good_bad p good_bad_predicted
bad 0.61624 bad
bad 0.03607 good
good 0.12437 good
good 0.21680 good
good 0.34833 good
good 0.69602 bad
bad 0.68873 bad
good 0.48351 good
good 0.03288 good
good 0.06789 good
good 0.61195 bad
good 0.15306 good
Confusion Matrix, 混淆矩阵
一个完美的分类模型就是,如果一个客户实际上 (Actual) 属于类别 good,也预测成(Predicted)good,处于类别 bad,也就预测成 bad。但从上面我们看到,一些实际上是 good 的客户,根据我们的模型,却预测他为 bad,对一些原本是 bad 的客户,却预测他为 good。我们需要知道,这个模型到底预测对了多少,预测错了多少,混淆矩阵就把所有这些信息,都归到一个表里:
| 预测 | ||||
|---|---|---|---|---|
| 1 | 0 | |||
| 实 | 1 | d, True Positive | c, False Negative | c+d, Actual Positive |
| 际 | 0 | b, False Positive | a, True Negative | a+b, Actual Negative |
| b+d, Predicted Positive | a+c, Predicted Negative |
其中,
- a 是正确预测到的负例的数量, True Negative(TN,0->0)
- b 是把负例预测成正例的数量, False Positive(FP, 0->1)
- c 是把正例预测成负例的数量, False Negative(FN, 1->0)
- d 是正确预测到的正例的数量, True Positive(TP, 1->1)
- a+b 是实际上负例的数量,Actual Negative
- c+d 是实际上正例的个数,Actual Positive
- a+c 是预测的负例个数,Predicted Negative
- b+d 是预测的正例个数,Predicted Positive
以上似乎一下子引入了许多概念,其实不必像咋一看那么复杂,有必要过一下这里的概念。实际的数据中,客户有两种可能 {good, bad},模型预测同样这两种可能,可能匹配可能不匹配。匹配的好说,0->0(读作,实际是 Negative,预测成 Negative),或者 1->1(读作,实际是 Positive,预测成 Positive),这就是 True Negative(其中 Negative 是指 预测成 Negative)和 True Positive(其中 Positive 是指 预测成 Positive)的情况。
同样,犯错也有两种情况。实际是 Positive,预测成 Negative (1->0) ,这就是 False Negative;实际是 Negative,预测成 Positive (0->1) ,这就是 False Positive;
我们可以通过 SAS 的 proc freq 得到以上数字:
proc freq data=valid_p;
tables good_bad*good_bad_predicted/nopercent nocol norow;
run;
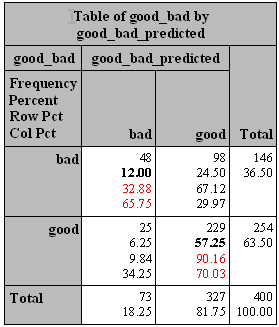
对照上表,结果如下:
预测
1 0
实 1,bad d, True Positive,48 c, False Negative,98 c+d, Actual Positive,146
际 0,good b, False Positive,25 a, True Negative,229 a+b, Actual Negative,254
b+d, Predicted Positive,73 a+c, Predicted Negative,327 400
根据上表,以下就有几组常用的评估指标(每个指标分中英文两行):
1. 准确(分类)率 VS. 误分类率
准确(分类)率 = 正确预测的正反例数 / 总数
Accuracy=true positive and true negative/total cases= a+d/a+b+c+d=(48+229)/(48+98+25+229)=69.25%
误分类率 = 错误预测的正反例数 / 总数
Error rate=false positive and false negative/total cases=b+c/a+b+c+d=1-Accuracy=30.75%
2. (正例的)覆盖率 VS. (正例的)命中率
覆盖率 = 正确预测到的正例数 / 实际正例总数,
Recall(True Positive Rate,or Sensitivity)=true positive/total actual positive=d/c+d=48/(48+98)=32.88%
注:覆盖率 (Recall)这个词比较直观,在数据挖掘领域常用。因为感兴趣的是正例 (positive),比如在信用卡欺诈建模中,我们感兴趣的是有高欺诈倾向的客户,那么我们最高兴看到的就是,用模型正确预测出来的欺诈客户 (True Positive)cover 到了大多数的实际上的欺诈客户,覆盖率,自然就是一个非常重要的指标。这个覆盖率又称 Sensitivity, 这是生物统计学里的标准词汇,SAS 系统也接受了(谁有直观解释?)。 以后提到这个概念,就表示为, Sensitivity(覆盖率,True Positive Rate)。
命中率 = 正确预测到的正例数 / 预测正例总数
Precision(Positive Predicted Value,PV+)=true positive/ total predicted positive=d/b+d=48/(48+25)=65.75%
注:这是一个跟覆盖率相对应的指标。对所有的客户,你的模型预测,有 b+d 个正例,其实只有其中的 d 个才击中了目标(命中率)。在数据库营销里,你预测到 b+d 个客户是正例,就给他们邮寄传单发邮件,但只有其中 d 个会给你反馈(这 d 个客户才是真正会响应的正例),这样,命中率就是一个非常有价值的指标。 以后提到这个概念,就表示为 PV+(命中率,Positive Predicted Value)。
3.Specificity VS. PV-
负例的覆盖率 = 正确预测到的负例个数 / 实际负例总数
Specificity(True Negative Rate)=true negative/total actual negative=a/a+b=229/(25+229)=90.16%
注:Specificity 跟 Sensitivity(覆盖率,True Positive Rate)类似,或者可以称为 “负例的覆盖率”,也是生物统计用语。以后提到这个概念,就表示为 Specificity(负例的覆盖率,True Negative Rate) 。
负例的命中率 = 正确预测到的负例个数 / 预测负例总数
Negative predicted value(PV-)=true negative/total predicted negative=a/a+c=229/(98+229)=70.03%
注:PV - 跟 PV+(命中率,Positive Predicted value)类似,或者可以称为 “负例的命中率”。 以后提到这个概念,就表示为 PV-(负例的命中率,Negative Predicted Value)。
以上 6 个指标,可以方便地由上面的提到的 proc freq 得到:
proc freq data=valid_p;
tables good_bad*good_bad_predicted;
run;
其中,准确率 = 12.00%+57.25%=69.25% ,覆盖率 = 32.88% ,命中率 = 65.75% ,Specificity=90.16%,PV-=70.03% 。
或者,我们可以通过 SAS logistic 回归的打分程序(score)得到一系列的 Sensitivity 和 Specificity,
proc logistic data=train;
model good_bad=checking history duration savings property;
score data=valid outroc=valid_roc;
run;
数据 valid_roc 中有几个我们感兴趣的变量:
PROB:阈值,比如以上我们选定的 0.5SENSIT:sensitivity(覆盖率,true positive rate)1MSPEC:1-Specificity,为什么提供 1-Specificity 而不是 Specificity,下文有讲究。
_PROB_ _SENSIT_ _1MSPEC_
0.54866 0.26712 0.07087
0.54390 0.27397 0.07874
0.53939 0.28767 0.08661
0.52937 0.30137 0.09055
0.51633 0.31507 0.09449
0.50583 0.32877 0.09843
0.48368 0.36301 0.10236
0.47445 0.36986 0.10630
如果阈值选定为 0.50583,sensitivity(覆盖率,true positive rate)就为 0.32877,Specificity 就是 1-0.098425=0.901575,与以上我们通过列联表计算出来的差不多(阈值 0.5)。
下期预告:ROC
以上我们用列联表求覆盖率等指标,需要指定一个阈值(threshold)。同样,我们在 valid_roc 数据中,看到针对不同的阈值,而产生的相应的覆盖率。我们还可以看到,随着阈值的减小(更多的客户就会被归为正例),sensitivity 和 1-Specificity 也相应增加(也即 Specificity 相应减少)。把基于不同的阈值而产生的一系列 sensitivity 和 Specificity 描绘到直角坐标上,就能更清楚地看到它们的对应关系。由于 sensitivity 和 Specificity 的方向刚好相反,我们把 sensitivity 和 1-Specificity 描绘到同一个图中,它们的对应关系,就是传说中的 ROC 曲线,全称是 receiver operating characteristic curve,中文叫 “接受者操作特性曲线”。欲知后事如何,且听下回分解。
参考资料:
- Mithat Gonen. 2007. Analyzing Receiver Operating Characteristic Curves with SAS. Cary, NC: SAS Institute Inc.
- Dan Kelly, etc. 2007. Predictive Modeling Using Logistic Regression Course Notes. Cary, NC: SAS Institute Inc.
- Confusion Matrix

发表 / 查看评论