开篇词

首先非常感谢COS论坛提供了这样一个良好的平台，敝人心存感激之余，也打算把一些学习心得拿出来供大家分享，文中纰漏之处还请各位老师指正。下面我将以WinBUGS的统计应用为题，分几次来谈一谈WinBUGS这个软件。其中会涉及到空间数据的分析、GeoBUGS的使用、面向R及SPLUS的接口包R2WinBUGS的使用、GIS与统计分析等等衍生出的话题。如有问题，请大家留下评论，我会调整内容，择机给予回答。

第一节 什么是WinBUGS?

WinBUGS对于研究Bayesian统计分析的人来说，应该不会陌生。至少对于MCMC方法是不陌生的。WinBUGS (Bayesian inference Using Gibbs Sampling）就是一款通过MCMC方法来分析复杂统计模型的软件。其基本原理就是通过Gibbs sampling和Metropolis算法，从完全条件概率分布中抽样，从而生成马尔科夫链，通过迭代，最终估计出模型参数。引入Gibbs抽样与MCMC的好处是不言而喻的，就是想避免计算一个具有高维积分形式的完全联合后验概率公布，而代之以计算每个估计参数的单变量条件概率分布。具体的算法思想，在讲到具体问题的时候再加以叙述，在此不过多论述。就不拿公式出来吓人了（毕竟打公式也挺费劲啊）。

第二节 为什么要用WinBUGS?

第一、因为同类分析软件中它做得最好。同类的软件：OpenBUGS、JAGS等在成熟度、灵活性以及兼容性方面和它相比还有一定距离。在处理spatial data的方面，它采用了Gibbs抽样和MCMC的方法，在模型支持方面又具有极大的灵活性，较之名声大噪的GeoR包，虽然也实现了bayesian的手法，但是灵活性还是不及WinBUGS。

第二、因为它免费。免费的东西总有吸引人之处。

第三、有各色的R包为WinBUGS实现了针对R的、SPLUS的、Matlab的软件接口。只要你喜欢，就直接在R下调用WinBUGS吧，无非是装个R2WinBUGS包，简简单单。

第四、详细的文档、帮助、指导、范例。当然没有中文版的，小小一点遗憾。

第三节 如何得到WinBUGS?

WinBUGS目前是一款免费的软件，去https://www.mrc-bsu.cam.ac.uk/software/bugs/下载就好了。不过要用高级功能（如GeoBUGS）的话，还是去http://www.mrc-bsu.cam.ac.uk/bugs/winbugs/contents.shtml注册一下好了^[编者注：该链接已失效，GeoBUGS1.2目前被打包到了WinBUGS1.4.1中，不需要额外注册]，挺方便的。系统会立即把注册码发到你邮箱（真是好人啊）。不过只可以用一个月。这倒无妨，到时在注册一下就好了。

第四节 初试WinBUGS

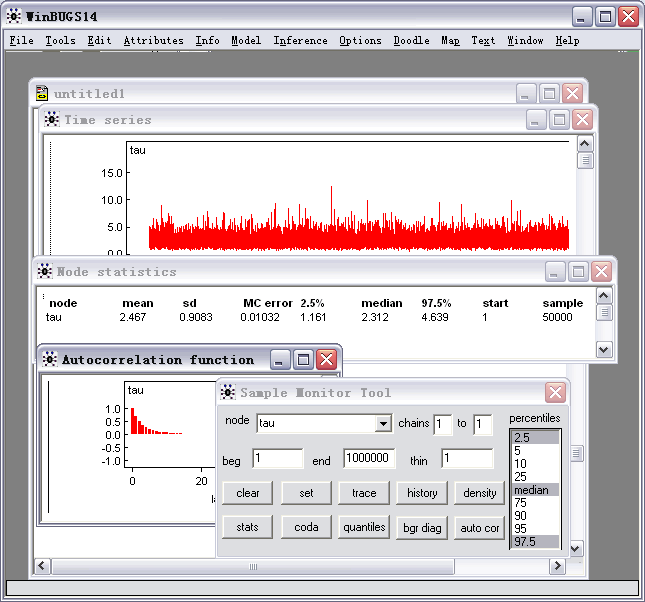
我们先找一个例子来实际地运行一下WinBUGS，感受一下基本的操作流程，然后再考虑高级的操作。

第一步，打开WinBUGS，通过菜单File -> New新建一个空白的窗口

第二步，在第一步中新建的空白窗口中输入三部分内容：模型定义、数据定义、初始值定义（代码见附录）

第三步，点击菜单Model -> Specification，弹出一个Specification Tool面板。

第四步，在第二步中的提到的那个窗口中，将model这个关键字高亮起来，点击check model。你会看到WinBUGS的左下角状态栏上显示“model is syntactically correct.”

第五步，把定义的data前的关键字list也高亮起来，点Specification Tool面板上的load data

第六步，改Specification Tool面板上的马尔科夫链的数目，默认为1就好了

第七步，点击Specification Tool面板上的compile

第八步，把定义的初始值中的list关键字也高亮起来，再点击Specification Tool面板上的load inits

第九步，关了Specification Tool面板

第十步，点击菜单Inference -> Samples，弹出一个Sample Monitor Tool面板。

第十一步，在Sample Monitor Tool面板的node中填要估计的参数名，这里可以是tau, alpha0, alpha1, b, 把它们一个一个填在node中，逐一点set。

第十二步，关了Sample Monitor Tool面板

第十三步，点击菜单Model -> Update，弹出一个Update Tool面板。

第十四步，将Update Tool面板中的updates改大点，比如50000，点update按钮。

第十五步，运行完后，关了Update Tool面板

第十六步，点击菜单Inference -> Samples

第十七步，在弹出的Sample Monitor Tool面板上选一个node

第十八步，点history看所有迭代的时间序列图，点trace看最后一次迭代的时间序列图，点auto cor看correlogram时间序列图，点stat看参数估计的结果

附第二步中的代码如下：

#MODEL
model
{
    for (i in 1:N) {
        O[i] ~ dpois(mu[i])
        log(mu[i]) <- log(E[i]) + alpha0 + alpha1 * X[i]/10 +
            b[i]
        # Area-specific relative risk (for maps)
        RR[i] <- exp(alpha0 + alpha1 * X[i]/10 + b[i])
    }
    # CAR prior distribution for random effects:
    b[1:N] ~ car.normal(adj[], weights[], num[], tau)
    for (k in 1:sumNumNeigh) {
        weights[k] <- 1
    }
    # Other priors:
    alpha0 ~ dflat()
    alpha1 ~ dnorm(0, 1e-05)
    tau ~ dgamma(0.5, 5e-04)
    # prior on precision
    sigma <- sqrt(1/tau)
    # standard deviation
}
#DATA

list(N = 56, O = c(9, 39, 11, 9, 15, 8, 26, 7, 6,
    20, 13, 5, 3, 8, 17, 9, 2, 7, 9, 7, 16, 31, 11, 7, 19, 15,
    7, 10, 16, 11, 5, 3, 7, 8, 11, 9, 11, 8, 6, 4, 10, 8, 2,
    6, 19, 3, 2, 3, 28, 6, 1, 1, 1, 1, 0, 0), E = c(1.4, 8.7,
    3, 2.5, 4.3, 2.4, 8.1, 2.3, 2, 6.6, 4.4, 1.8, 1.1, 3.3, 7.8,
    4.6, 1.1, 4.2, 5.5, 4.4, 10.5, 22.7, 8.8, 5.6, 15.5, 12.5,
    6, 9, 14.4, 10.2, 4.8, 2.9, 7, 8.5, 12.3, 10.1, 12.7, 9.4,
    7.2, 5.3, 18.8, 15.8, 4.3, 14.6, 50.7, 8.2, 5.6, 9.3, 88.7,
    19.6, 3.4, 3.6, 5.7, 7, 4.2, 1.8), X = c(16, 16, 10, 24,
    10, 24, 10, 7, 7, 16, 7, 16, 10, 24, 7, 16, 10, 7, 7, 10,
    7, 16, 10, 7, 1, 1, 7, 7, 10, 10, 7, 24, 10, 7, 7, 0, 10,
    1, 16, 0, 1, 16, 16, 0, 1, 7, 1, 1, 0, 1, 1, 0, 1, 1, 16,
    10), num = c(3, 2, 1, 3, 3, 0, 5, 0, 5, 4, 0, 2, 3, 3, 2,
    6, 6, 6, 5, 3, 3, 2, 4, 8, 3, 3, 4, 4, 11, 6, 7, 3, 4, 9,
    4, 2, 4, 6, 3, 4, 5, 5, 4, 5, 4, 6, 6, 4, 9, 2, 4, 4, 4,
    5, 6, 5), adj = c(19, 9, 5, 10, 7, 12, 28, 20, 18, 19, 12,
    1, 17, 16, 13, 10, 2, 29, 23, 19, 17, 1, 22, 16, 7, 2, 5,
    3, 19, 17, 7, 35, 32, 31, 29, 25, 29, 22, 21, 17, 10, 7,
    29, 19, 16, 13, 9, 7, 56, 55, 33, 28, 20, 4, 17, 13, 9, 5,
    1, 56, 18, 4, 50, 29, 16, 16, 10, 39, 34, 29, 9, 56, 55,
    48, 47, 44, 31, 30, 27, 29, 26, 15, 43, 29, 25, 56, 32, 31,
    24, 45, 33, 18, 4, 50, 43, 34, 26, 25, 23, 21, 17, 16, 15,
    9, 55, 45, 44, 42, 38, 24, 47, 46, 35, 32, 27, 24, 14, 31,
    27, 14, 55, 45, 28, 18, 54, 52, 51, 43, 42, 40, 39, 29, 23,
    46, 37, 31, 14, 41, 37, 46, 41, 36, 35, 54, 51, 49, 44, 42,
    30, 40, 34, 23, 52, 49, 39, 34, 53, 49, 46, 37, 36, 51, 43,
    38, 34, 30, 42, 34, 29, 26, 49, 48, 38, 30, 24, 55, 33, 30,
    28, 53, 47, 41, 37, 35, 31, 53, 49, 48, 46, 31, 24, 49, 47,
    44, 24, 54, 53, 52, 48, 47, 44, 41, 40, 38, 29, 21, 54, 42,
    38, 34, 54, 49, 40, 34, 49, 47, 46, 41, 52, 51, 49, 38, 34,
    56, 45, 33, 30, 24, 18, 55, 27, 24, 20, 18), sumNumNeigh = 234)
#INITIAL VALUES
list(tau = 1, alpha0 = 0, alpha1 = 0, b = c(0, 0,
    0, 0, 0, NA, 0, NA, 0, 0, NA, 0, 0, 0, 0, 0, 0, 0, 0, 0,
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
    0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0))

WinBUGS在统计分析中的应用 第一部分完