统计应用

WinBUGS在统计分析中的应用（第二部分）

齐韬

关键词：SAS; WinBUGS; 贝叶斯

第一节 WinBUGS数据分析案例

在这一节中，我将拿一个经典的研究数据，利用WinBUGS给出简单的分析。首先介绍一下这个数据：Seeds

seed O. aegyptiaco 75 	seed O. aegyptiaco 73	Bean 	Cucumber 	Bean 	Cucumber
r 	n 	r/n 	r 	n 	r/n 	r 	n 	r/n 	r 	n 	r/n
10 	39 	0.26 	5 	6 	0.83 	8 	16 	0.5 	3 	12 	0.25
23 	62 	0.37 	53 	74 	0.72 	10 	30 	0.33 	22 	41 	0.54
23 	81 	0.28 	55 	72 	0.76 	8 	28 	0.29 	15 	30 	0.5
26 	51 	0.51 	32 	51 	0.63 	23 	45 	0.51 	32 	51 	0.63
17 	39 	0.44 	46 	79 	0.58 	0 	4 	0 	3 	7 	0.43
10 	13 	0.77

这个数据来自Crowder (1978)。之后Breslow and Clayton (1993) 作为例子，也分析过这个数据。数据反映的是某一品种的豆类种子和某一品种的黄瓜种子，分别放在21个培养皿（plates）中分别培养，在根提取物aegyptiaco 75和aegyptiaco 73的作用下的出芽率的差异。其中r是出芽的个数，n是种子的个数，而r/n是出芽率。我们用random effect logistic regression模型来进行分析（注意，在Bayesian分析中，通常是将covariates看做是服从某一个分布的随机变量，这和一般意义上的GLM, GLME, LME中对于covariates解释是不同的）：

\(r_i \sim Binomial(p_i, ~n_i)\)

\(logit(p_i)=\alpha_0 + \alpha_1 x_{1i} + \alpha_2 x_{2i} + \alpha_{12} x_{1i} x_{2i} + b_i\)

\(b_i \sim Normal(0, \tau)\)

其中\(x_{1i}\)是种子的类型，\(x_{2i}\)是根提取物的类型，\(\alpha_{12} x_{1i} x_{2i}\)是交互项, \(\alpha_0,~\alpha_1,~\alpha_2,~\alpha_{12},~\tau\)是给定的独立的 “noninformative” 先验参数。在Bayesian分析中，通常我们会定义一个DAG图(即Directed Acyclic Graph有向无圈图) 。我们可以在WinBUGS中通过设计DAG图来定义模型。不过这一节中我们还是用WinBUGS中的BUGS语言来定义模型，如何在WinBUGS中通过设计DAG图来定义模型我将在下一节中详细介绍，但是必须要说明的是BUGS语言比DAG图灵活，不过直观性不如后者。

模型

model
{
 for( i in 1 : N ) {
  r[i] ~ dbin(p[i],n[i])
  b[i] ~ dnorm(0.0,tau)
  logit(p[i]) <- alpha0 + alpha1 * x1[i] + alpha2 * x2[i] +
   alpha12 * x1[i] * x2[i] + b[i]
 }
 alpha0 ~ dnorm(0.0,1.0E-6)
 alpha1 ~ dnorm(0.0,1.0E-6)
 alpha2 ~ dnorm(0.0,1.0E-6)
 alpha12 ~ dnorm(0.0,1.0E-6)
 tau ~ dgamma(0.001,0.001)
 sigma <- 1 / sqrt(tau)
}

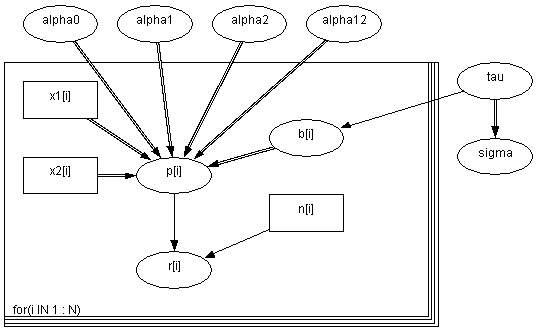WinBUGS doodle模型 WinBUGS doodle模型

数据

list(r = c(10, 23, 23, 26, 17, 5, 53, 55, 32, 46, 10,   8, 10,   8, 23, 0,  3, 22, 15, 32, 3),
   n = c(39, 62, 81, 51, 39, 6, 74, 72, 51, 79, 13, 16, 30, 28, 45, 4, 12, 41, 30, 51, 7),
   x1 = c(0,   0,  0,   0,   0, 0,   0,   0,  0,   0,   0,  1,   1,   1,   1, 1,   1,  1,   1,   1, 1),
   x2 = c(0,   0,  0,   0,   0, 1,   1,   1,  1,   1,   1,  0,   0,   0,   0, 0,   1,  1,   1,   1, 1),
   N = 21)

初始值

list(alpha0 = 0, alpha1 = 0, alpha2 = 0, alpha12 = 0, tau = 1)

经过10000次迭代，我们得到参数的估计如下：

node    mean     sd MC error   2.50%  median  97.50% start
 alpha0 -0.5546 0.1941 0.007696 -0.9353 -0.5577 -0.1597  1001
 alpha1 0.08497 0.3127  0.01283 -0.5814 0.09742  0.6679  1001
alpha12 -0.8229 0.4321  0.01785  -1.697 -0.8218 0.01641  1001
 alpha2   1.356 0.2743  0.01236  0.8257   1.347   1.909  1001
  sigma  0.2731 0.1437 0.007956 0.04133  0.2654  0.5862  1001

第二节 结合SAS做比较分析

下面我们用同样的数据在SAS中进行分析，看看结果相差多少：

首先生成数据：

data seeds;
 input plate r n seed extract;
 datalines;
1   10  39  0   0
2   23  62 0   0
3   23  81 0   0
4   26  51 0   0
5   17  39 0   0
6    5   6  0   1
7   53  74 0   1
8   55  72 0   1
9   32  51 0   1
10  46  79 0   1
11  10  13 0   1
12   8  16 1   0
13  10  30 1   0
14   8  28 1   0
15  23  45 1   0
16   0   4  1   0
17   3  12 1   1
18  22  41 1   1
19  15  30 1   1
20  32  51 1   1
21   3   7  1   1
;
run;
data seeds;
 set seeds;
 interact=seed*extract;
run;
proc print; run;

然后调用GENMOD过程，拟合经典的logistic regression回归模型

proc genmod data=seeds;
/* Basic logistic regression WHITHOUT random plate effect */
title ‘Classical logistic regression’;
 model r/n= seed extract interact / dist=B;
run;

得到

Analysis Of Parameter Estimates
Parameter	DF	Estimate	Standard Error	Wald 95% Confidence Limits	Chi-Square	Pr > ChiSq
Intercept	1	-0.5582		0.126		-0.8052	-0.3112			19.62	     	<.0001
seed		1	0.1459		0.2232		-0.2915	0.5833			0.43		0.5132
extract		1	1.3182		0.1775		0.9704	1.666			55.17	      	<.0001
interact	1	-0.7781		0.3064		-1.3787	-0.1775			6.45		0.0111
Scale		0	1		0		1	1

调用NLMIXED过程，拟合经典的logistic regression回归模型

proc nlmixed data=seeds;
/* Cassical logistic regression using NLMIXED */
title 'Classical logistic regression with NLMIXED';
parms b0=-0.55 b1=0.15 b2=1.32 b12=-0.78;
logitp=b0+b1*seed+b2*extract+b12*interact;
p=exp(logitp)/(1+exp(logitp));
model r ~ binomial(n,p) ;
run;

得到：

Parameter Estimates
Parameter	Estimate	Standard Error	DF	t Value	Pr > |t|	Alpha	Lower	Upper	Gradient
b0		-0.5582		0.126		21	-4.43	0.0002		0.05	-0.8202	-0.2961	-0.00000229
b1		0.1459		0.2232		21	0.65	0.5203		0.05	-0.3182	0.61	-8.82E-07
b2		1.3182		0.1775		21	7.43	<.0001		0.05	0.9491	1.6872	-0.00000161
b12		-0.7781		0.3064		21	-2.54	0.0191		0.05	-1.4154	-0.1408	-6.61E-07

调用NLMIXED过程，拟合经典带随机截距的logistic regression回归模型

proc nlmixed data=seeds;
/* Logistic regression + RANDOM plate INTERCEPT */
title 'Logistic regression with random plate intercept (NLMIXED)';
parms b0=-0.55 b1=0.15 b2=1.32 b12=-0.78;
logitp=b0+b1*seed+b2*extract+b12*interact+alpha;
p=exp(logitp)/(1+exp(logitp));
random alpha ~ normal(0,varu) subject=plate out=seedmixed;
model r ~ binomial(n,p) ;
run;

得到：

Parameter Estimates
Parameter	Estimate	Standard Error	DF	t Value	Pr > |t|	Alpha	Lower	Upper	Gradient
b0		-0.5484		0.1666		20	-3.29	0.0036		0.05	-0.896	-0.2009	-0.00087
b1		0.097		0.278		20	0.35	0.7308		0.05	-0.483	0.677	0.00022
b2		1.337		0.2369		20	5.64	<.0001		0.05	0.8428	1.8313	-0.00018
b12		-0.8104		0.3852		20	-2.1	0.0482		0.05	-1.6139	-0.007	0.00037
1.07		0.295 varu	0.05581		0.05	20	9		0.05	-0.0527	0.1643	0.001515

当然了winBUGS的强大之处并不在于此，而是在处理诸如GLME（有些文献称GLMM），空间数据模型等计算复杂的模型，之后还会继续讨论。

参考文献：

[1] Crowder M J (1978) Beta-binomial Anova for proportions. Applied Statistics. 27, 34-37.

[2] Breslow N E and Clayton D G (1993) Approximate inference in generalized linear mixed models. Journal of the American Statistical Association. 88, 9-25.

最后再送出一本书，供大家研究参考

Disease Mapping with WINBUGS and MLWin（djvu格式）

WinBUGS在统计分析中的应用 第二部分完

敬告各位友媒，如需转载，请与统计之都小编联系（直接留言或发至邮箱：editor@cos.name），获准转载的请在显著位置注明作者和出处（转载自：统计之都），并在文章结尾处附上统计之都微信二维码。

统计之都微信二维码

发表/查看评论