回归分析往往是学统计、学计量课程时接触的第一个统计模型了,甚至不少人可能认为回归分析理所当然成为计量的绝大部分内容——毕竟很多教材中提到统计模型的时候,往往就一个OLS为主的讲法。回归分析的内容当然很广泛,也在学科中占据相对基础的位置。
学会OLS,有人还明白了ML等方法的含义;现在学统计分析的时候,或多或少会安排统计软件的实践课程,于是大家学会了使用Excel,乃至SAS中如何来做经典的回归分析。看过不少的文献,很多都忽略了回归分析模型诊断这个环节——可能很多标准教科书没有强调,甚至是没有讲;这不能不说是一个遗憾。
回归分析使用最广泛,误用的情况也多了些。下面使用一个经典的例子,来“恶心”一下那些“过分钟爱”经典回归分析的人——我在很多课堂上都举过这个例子(Anscombe),作为从基础课程向中级乃至高级课程的开场白。
x1 x2 x3 x4 y1 y2 y3 y4
1 10 10 10 8 8.04 9.14 7.46 6.58
2 8 8 8 8 6.95 8.14 6.77 5.76
3 13 13 13 8 7.58 8.74 12.74 7.71
4 9 9 9 8 8.81 8.77 7.11 8.84
5 11 11 11 8 8.33 9.26 7.81 8.47
6 14 14 14 8 9.96 8.10 8.84 7.04
7 6 6 6 8 7.24 6.13 6.08 5.25
8 4 4 4 19 4.26 3.10 5.39 12.50
9 12 12 12 8 10.84 9.13 8.15 5.56
10 7 7 7 8 4.82 7.26 6.42 7.91
11 5 5 5 8 5.68 4.74 5.73 6.89
上面有四对x,y,分别做经典回归分析的话,结果如下:
[[1]]
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.0000909 1.1247468 2.667348 0.025734051
x1 0.5000909 0.1179055 4.241455 0.002169629
[[2]]
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.000909 1.1253024 2.666758 0.025758941
x2 0.500000 0.1179637 4.238590 0.002178816
[[3]]
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.0024545 1.1244812 2.670080 0.025619109
x3 0.4997273 0.1178777 4.239372 0.002176305
[[4]]
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.0017273 1.1239211 2.670763 0.025590425
x4 0.4999091 0.1178189 4.243028 0.002164602
这时候你会发现p值、s.e.值都好的很,截距项和斜率项也非常好,甚至连R square都简直一模一样。
往往讲到这个时候,机灵点的学生就开始皱眉头了:数据差别挺大的,怎么模型都是一样呢!?
学过回归诊断的人立刻就嚷嚷来做个回归诊断来看看,四种情况下是不是有的属于“模型前提假设”不满足的情况。(当然,似乎本科阶段,教师没有过分强调这点的,很少有学生能自己自主的想到这点,所以往往让人感叹教学过程中的不完善。)
紧接着我就给他们做出一幅图:
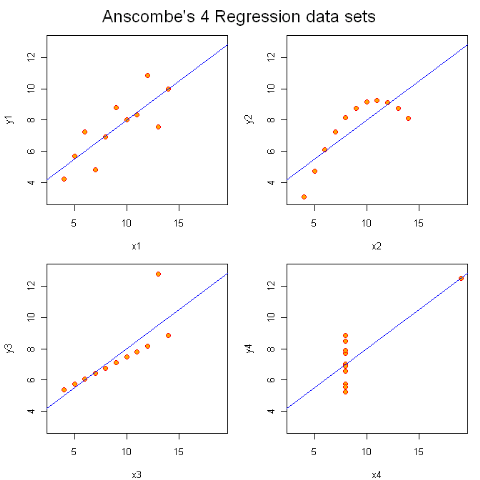
这时候他们有点明白,能回答说左上是我们“常见”的回归;右上完全就是二次曲线嘛;左下存在一个“异常点”;而右下,完全就属于“诡异”情形。
所以可以归纳一下:做统计模型的时候,一定记得要模型诊断下——重点就分析下残差是不是符合假设——这个是标准套路。如果你想“偷懒”,在只有一个自变量的时候,不妨在样本量不多(现在的统计软件已经非常强大了,数万对点很容易搞定;如果数据太多,你也可以抽样来试试嘛。)这样,“一眼”就能看出个大概了——这恐怕就是人比机器厉害的地方,人比模型厉害的地方。

发表/查看评论