相关系数阵对于分析多元数据时非常有用，然而当变量较多时，我们很难从一堆庞大的数字中快速获取信息。正因为如此，相关阵的可视化应运而生。的确，活泼生动的图形对我们的眼球更有诱惑力。已有的相关阵可视化技巧有颜色图、椭圆图、钟表图(参见Deepayan Sarkar所著的《Multivariate Data Visualization with R》中的Fig13.6)等，其思想都非常直观。本文在阐述了颜色图和椭圆图的机理后，又提出了一种新的相关阵的可视化技术——圆圈图，并与颜色图、椭圆图进行了比较。

2010-4-11更新:本文及扩展工作对应的包corrplot可从CRAN下载。

颜色图

颜色图就是将一个网格矩阵映射到指定的颜色序列上，恰当地选取颜色来展示数据。在相关阵中，所有的数据都在 -1 到 1 之间，我们不仅要关注相关系数的绝对值大小，同时更加看重它们的正负号。因此，相关阵的颜色图和一般矩阵的颜色图应该有所区别：即应当选取两种色差较大的颜色序列来展示不同符号的相关系数， Gregor Gorjanc 建议用蓝色表示正相关系数，红色表示负相关系数。

R 中，image()函数可以轻松绘制颜色图，利用 mcars 数据，下面代码可以得到其加了相关系数(乘以100，是为了节省空间)的颜色图（图1）。

data(mtcars)
fit = lm(mpg ~ ., mtcars)
cor = summary(fit, correlation = TRUE)$correlation
#相关阵上下倒转再转置，是为了让画出的图和相关阵方向一致
cor2 = t(cor[11:1, ])
#下面颜色取自ellipse包中的plotcorr函数的示例
colors = c("#A50F15", "#DE2D26", "#FB6A4A", "#FCAE91", "#FEE5D9",
	"white", "#EFF3FF", "#BDD7E7", "#6BAED6", "#3182BD", "#08519C")
image(1:11, 1:11, cor2, axes = FALSE, ann = F, col = colors)
text(rep(1:11, 11), rep(1:11, each = 11), round(100 * cor2))

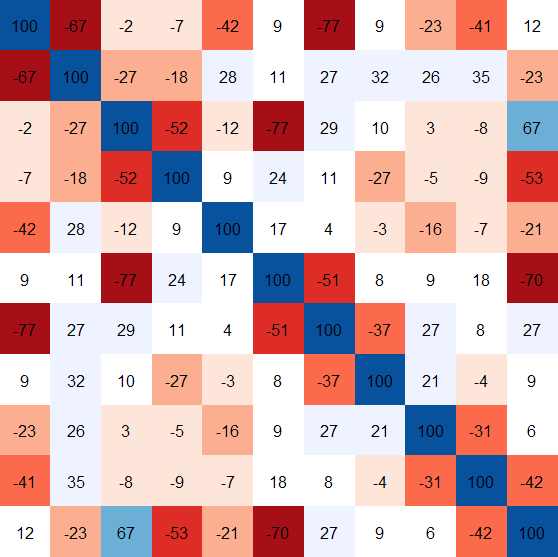
图1 相关阵的颜色图

观察图1，通过颜色的比较，可以直观看出相关系数的符号和大小：深色区域表示较强相关性，浅色区域表示较弱的相关性。

椭圆图

椭圆图是利用椭圆的形状来表示相关系数：离心率越大，即椭圆越扁，对应绝对值较大的相关系数；离心率越小，即椭圆越圆，对应绝对值较小的相关系数。椭圆长轴的方向来表示相关系数的正负：右上-左下方向对应正值，左上－右下方向对应负值。当然

R 中，ellipse包中的plotcorr() 可以实现这一功能，同样利用 mcars 数据，来展示椭圆图（图2）。他山之石，可以攻玉，椭圆图当然可以利用色彩来增强表现力。

library(ellipse)
col = colors[as.vector(apply(corr, 2, rank))]
plotcorr(cor, col = col, mar = rep(0, 4))

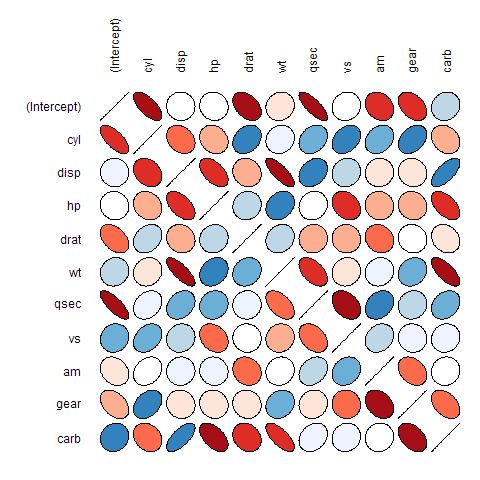
图2. 相关阵的椭圆图

观察图2，可以发现尽管所有椭圆披红挂蓝，但该图并不是非常形象生动（本文前一个版本中所有椭圆皆为灰色，表现力更差）。

圆圈图

考虑到前两种方法的局限性，本人设计了一种新的相关阵的可视化方法——圆圈图。具体做法是：

1. 用圆的面积来表示相关矩阵的绝对值大小。 1.用实心圆(圆内填充颜色)和空心圆来表示相关系数的正负号。

下面编写函数（最终版见R Graph Gallery）绘图，仍基于mcars数据，得到圆圈图(图3)。

circle.cor=function(cor,axes=FALSE, xlab='', ylab='', asp=1,
		title="Taiyun's cor-matrix circles",...){
     n=nrow(cor)
     cor=t(cor[n:1,]) ##先上下倒转，再转置
     par(mar = c(0, 0, 2, 0), bg = "white")
     plot(c(0,n+0.8),c(0,n+0.8),axes=axes, xlab='', ylab='', asp=1, type='n')
     segments(rep(0.5,n+1),0.5+0:n, rep(n+0.5,n+1),0.5+0:n,col='gray')
     segments(0.5+0:n, rep(0.5,n+1), 0.5+0:n, rep(n+0.5,n),col='gray')
     for(i in 1:n){
	for(j in 1:n){
		c=cor[i, j]
		bg=switch(as.integer(c>0)+1,'white','black')
		symbols(i,j,circles=sqrt(abs(c))/2, add=TRUE, inches=F, bg=bg)
	}
     }
     text(rep(0,n),1:n,n:1,col='red')
     text(1:n,rep(n+1),1:n,col='red')
     title(title)
}
circle.cor(cor)

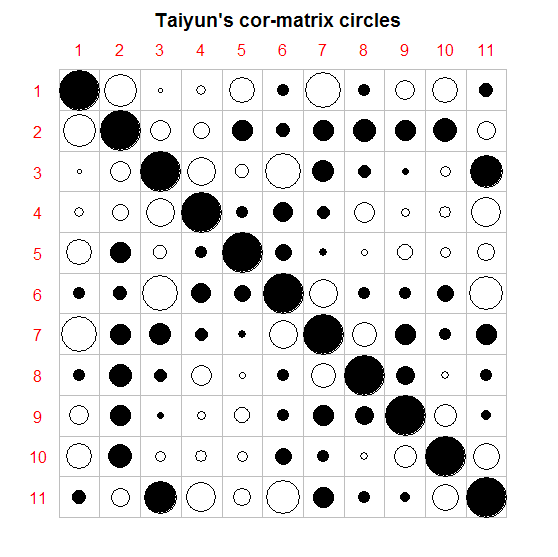
图3. 相关阵的圆圈图

图3 中，黑色实心圆表示正相关系数，空心圆表示负相关系数。观察图3 ，不难看出相关系数的大小、正负都空前清楚明了。

实际上，图3 还有发展空间，比如可以在图旁添加图例，用颜色信息辅助面积大小，或者将相关系数标在图上，还可以将该图分为上下两三角，留其一添加其他信息。但需要注意的是不可喧宾夺主。

讨论

1. 人们往往更为关注相关性较强的数据，从这一方面来看，椭圆图比较失败，因为它将最大的面积留给了相关性最弱的数据，给其他信息的获取造成了一定的干扰。而颜色图和圆圈图则较为成功，尤其是圆圈图。
2. 相关系数的正负号非常有价值，在从这方面来看，颜色图和椭圆图都比较失败。所谓“五色令人目盲”，当色彩过于纷呈时，我们往往会眼花缭乱，正负号各仅有其一，而颜色图中的颜色却远非如此(这对于色盲更为不利)。而椭圆图中，反映正负号的信息本来就是两个方向，不如圆圈图那样“黑白分明”，更糟的是这些信息受到了过多的干扰。
3. 综上，圆圈图的优点是：1.黑白分明，正负号一清二楚。2.圆的大小表示相关性强度，具有很好的可比性。3.照顾最广大人群(包括颜色不敏感者以及色盲患者)，方便打印，信息不易失真。4.将表现力的最强图形元素留给最有价值的数据(最大的圆留给相关系数最强的数据)，资源配置良好。5.简单明了，干扰信息最少。