从调查报告中的比例数字说统计人如何甄别统计假象

新华网刚发布了一个关于学生冬季长跑的调查结果（于2009年4月27日13:52访问），一共调查了100人，结果中却出现了92.79%这样的比例数字，有常识的读者都知道，世上不存在0.79个人，因此这里面必然有某个地方是错的（姑且不妄言造假）。这则消息让我马上想起《统计陷阱》这本书，我们生活中有多少陷阱呢？

从消息编辑人员的角度来说，他们可能觉得保留两位小数显得“精确”，而这种“精确精神”从数学的角度来说显得既可爱又可笑，如果小数位能表示精确，那何不保留100位小数呢？

从统计人的角度来看，对这种调查报告中的比例数字应该有足够的警觉。很多调查报告并不会告诉我们究竟样本量多大（在这一点上新华网的调查网还比较诚实），这种情况下，我们应该弄清究竟调查了多少对象，当样本量很小的时候我们会怀疑这个调查的代表性。当我们看到比例66%的时候也许能想起来这是2/3（猜测样本量是3的倍数），但对29.1667%这个比例我们未必能很快反应出来分子和分母是多少，若报告公布方没有说明样本量，我们只能自己猜测；对于667这样的数字，我们很容易猜测这是6循环的四舍五入。最终大概思路就是拿比例去挨个乘以一系列整数，看看哪个结果接近整数，从而“还原”原来的分式n/N。以下是简单的R代码：

> digit = ((1:100) * 0.29166666)%%1 # 整除1之后的“余数”
> plot(digit, ylim = c(0, 1))
> idx = which((1 - digit) < 1e-05 | (digit - 0) < 1e-05) # 与0或1很靠近时
> points(idx, digit[idx], pch = 20)
> abline(v = idx, lty = 2)
> axis(3, idx)
> idx * 0.29166666
[1]  7 14 21 28

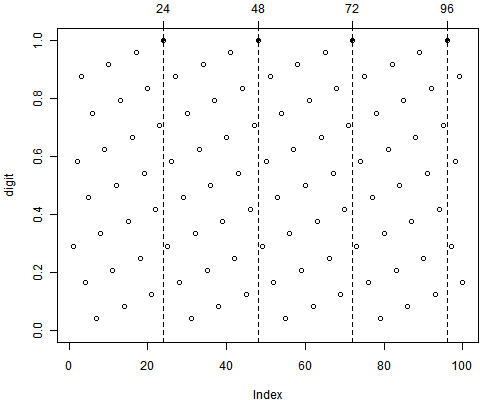
我们很容易发现分母（样本量）是24的倍数，因为上图中24的倍数乘以29.167%得到的结果很靠近整数；而具备某种特征的样本数量为7的倍数。根据具体的调查背景，我们可以自己猜测报告方究竟调查了多少人：24人？太少；960人？为什么不是1000人？……

上面只是统计侦查的小游戏而已，当我们具备更多统计知识储备之后，便可以去考虑一些具体的统计模型输出是否存在造假嫌疑。我想，P值在0.05之下且很靠近0.05的时候，或P值一律接近于0的时候，我们不妨以小人之心揣测这个模型也许有问题。当因子分析中，50个变量能根据载荷被准确划分到作者预先设定的5个因子中时（5列因子载荷一律都是只在某个因子上取值极大），这个分析也许存在嫌疑。当然，所有的“小人之心”的前提假设都是：理想情况在现实中是不容易出现的（这是赤裸裸的假设检验逻辑）。