引言——变量关系分析的广泛意义

在统计分析中，有这样一类具有普遍意义的问题：在测得了（取样）一个变量系统的数据以后，如何从数据中发现并且验证这些变量之间的关系？了解变量之间的关系，无论是对于知识发掘(knowledge discovery)，还是拟合精度的提高，都是很有意义的．比如任何一类回归分析，便是要分析预测变量和响应变量之间的关系．如果我们能用一些方法做回归前的预分析(pre-analysis before regression)，比如，使用方差分析去分析各个预测因素之间的关系，是非常有必要的．为什么呢？一个很简单的原因是出于对复线性的考虑．众所周知，复线性是回归分析的大敌．如果大家还记得回归分析系数的协方差矩阵的话，想必也能记得如果预测因素之间的相关系数太大会导致回归方程系数非常不稳定(请参阅 method of multivariate data analysis by rencher)．又如结构方程模型，是要分析测量变量(measurement)和结构变量(construct)之间的关系．还有最近十分热门的图模型，便是赤裸裸的声称图模型是所有统计模型的一个大综合．

变量关系的终极表示－因果关系

图模型里面大名鼎鼎的，来自人工智能的贝叶斯网络－－相信很多人都有所耳闻．如下是名为alarm network的一个贝叶斯网络的经典之作，被公认为是贝叶斯网络的实用性的一个证明：

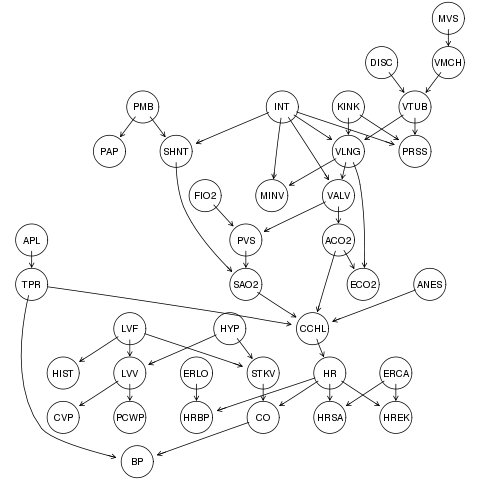
该网络是一个辅助医疗诊断系统．共涉及37个变量,46条边． 贝叶斯网络的一个显著特征是它所使用的箭头在很多情况下可以解读为＂因果关系＂－－当然，能否从面板数据中推演因果关系尚存在争议．但是目前我们仍然假设这种可能性．贝叶斯网络的理解很简单，并且已经有了从统计数据中训练一个贝叶斯网络的多种方法，因为流行程度达到了新一轮的高潮．但是，与它的流行伴随而来的是一个让人困扰的问题：贝叶斯网络的训练方法是在太慢(就我的经验，训练如上一个37个变量的网络大概需要3小时，6G 内存、4M 缓存条件下)．而且，算法本身经常陷入局部最优，而这些局部最优往往离真实模型相差甚远．特别是数据量不够的话，局部最优的点会很多，给算法本身的实用性提供了相当大的挑战．另外，对于一个贝叶斯网络的训练，需要大量的数据去支持．经典的多元统计理论认为，一般的多元模型参数与数据量的比值应当>20．但是通常大家认为，这个比率对于被噎死网络可能还太保守．

之所以在这里谈到贝叶斯网络，是为接下来的较为简单的模型或者数据分析树立一个远大的理想．现在我们的目标已经明确，那就是，在人类所能理解的范畴内，我们最好是能将系统内各个变量的关系用贝叶斯网络所表示出来，其中的箭头代表因果关系，或者至少也要代表一个先后关系，这是我们作数据分析，总结结论的一个终极目标．但是，所谓理想常常是与现实有所出入，在统计学界亦是如此－－从哲学角度来定义因果的话，那么有一条是因果关系所必须满足的，那就是原因是不可能出现在结果之后的．那么，如果我们想知道两者的因果关系，就需要我们知道一个重要的信息－－时序．而很可惜，这个信息并不是总能得到．而且，因果分析还需要一个更为严格的条件是：如果你需要推演一个系统内变量的因果关系的话，你必须保证这个系统内所有的变量都已经被测量(请参阅computation, cauality, and discovery)．这个还仅仅是一个必要条件．这就是为什么Fisher他老人家终生都反对吸烟导致肺癌的的原因了．下图是关于肺癌的研究的一个很经典的贝叶斯网络：

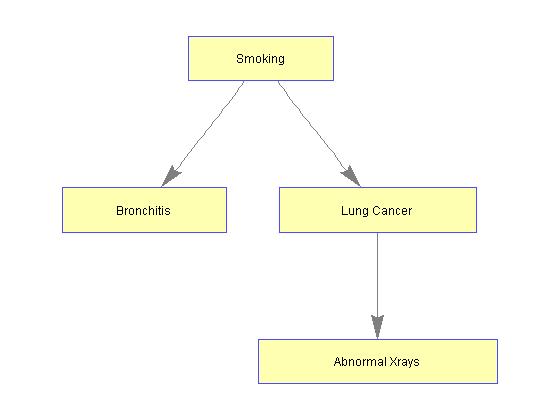
社会上传言：Fisher老人家是喜好抽烟的．他看到这个统计结果以后，立马就提出了一个另外的解释：根据当时收集的样本，人们并不能排除是否存在一种基因，是这种基因导致了意中人既喜欢抽烟，又容易得肺癌．统计上来看这个问题的话，就是在抽烟和肺癌之间还存在一个隐藏变量－Fisher所说的基因，导致了这两者之间是有关系的．而因为我们没有观测到这个变量，所以我们的最终模型里出现了一个从抽烟到肺癌的箭头．

Fisher所说并非狡辩．这也是他一直所声称的，观察研究（observational study）并不能获得因果关系的信息，而倘若研究目的是因果关系的话，那只有实验设计可能还有点戏．本文支持这一观点．但是本文也需要指出，从观察研究里推演因果关系是有可能的－－感兴趣的可以点击Pear的主页，Pearl乃是因果推断的一代宗师．具体的指导思想是－－我们可以从观测数据中推导各个变量之间的相关关系，再假设这些相关关系都是正确的，根据图论的一些理论，并且结合奥柯姆原理(occam’s principle，简单模型优先)我们就可以推导出部分因果关系．

贝叶斯网络的训练

如上一段所说，贝叶斯网络是符合人类逻辑思维的一种图模型，也是人类思维里表征知识的一种形式，因此广为人民群众所喜闻乐见．接下来的一个问题便是，如何能从数据中得到一个贝叶斯网络？

用人工智能里面的话来说，一个完整的贝叶斯网络包含两个元素，１）结构，也就是那些带有箭头的边；２）系数，也就是每条边的系数．如果所有的变量都是连续型，那我们可以假设它是一个多元高斯分布，于是每个系数就相当于解释变量和被解释变量之间的回归系数．从这里我们可以粗略的得到结论，那就是：倘若知道了结构，得到系数不难．所以贝耶斯网络的训练分两步走，先训练结构，在训练系数．但是问题是如何得到结构？有兴趣的朋友可以google如下关键词“PC Algorithm”, “IC Algorithm”,“K2 Algorithm” 以及 “learning of gaussian network by heckmen”.

另外，从实用角度出发，推荐两个工具箱．前者是贝叶斯网络以及隐马尔科夫模型的一个经典的MATLAB工具箱：Bayes Net Toolbox for Matlab.

另外还发现一个R的包：bnlearn，但我目前还没有用过．

结论

此文仅仅作为科普之用，欢迎拍砖．如果你感到无法满足，你可以点击这里，作者Kevin Murphy是图模型方面的一个牛人．如果你仍然不能满足，那么我推荐你google一下 “micheal jordan”(Kevin的老板)，可以发现更多与他一样牛的他的师兄弟师姐妹，有做马尔科夫网络, 隐马尔科夫模型, 动态贝叶斯网络， 独立成分分析（independent component analysis）, 状态空间模型等等，这些都属于图模型，并且都很有意思．

另外，正如文中所说，＂之所以在这里谈到贝叶斯网络，是为接下来的较为简单的模型或者数据分析树立一个远大的理想＂．可能在接下来的后续文章我会与大家讨论如下这种更加实际的情况：如果我们无法做因果分析，那该怎么办？我们仍然需要知道变量之间的关系，无论是为了知识发掘，还是寻求一个好的预测模型．这是一个更加广泛的话题，而且某种程度上可以作为贝叶斯网络的一种替代品．当然，有人可能会跳出来反驳说，并不是所有的统计分析的最终目标是是为了画一个贝叶斯网络.　总而言之，接下来的话题将与此不同．