本文是对R中精算学专用包actuar使用的一个简单教程。actuar项目开始于2005年,在2006年2月首次提供公开下载,其目的就是将一些常用的精算函数引入R系统。目前,提供的函数主要涉及风险理论,损失分布和信度理论。
如题所示,本文是我在学习actuar包过程中的学习笔记,主要涉及这个包中一些函数的使用方法和细节,对一些方法的结论也有稍许探讨,因此能简略的地方简略,而讨论的地方可能讲的会比较详细。闲话少提,下面正式开始学习!
1、数据分组
分组数据是精算学中常用的数据格式,比如我们要把不同风险类别的人群进行分别统计。假设我们要把一组连续变量分为n组,显然需n+1个边界。
函数
gouped.data(Group = c(...), freq1 = c(...), freq2 = c(...),
..., right = TRUE, row.names = NULL)
使用注意:
1) Group 是分组的临界值,freq1和freq2是对应组别的频数。Group,freq1和freq2可以随意命名,但是一定要把临界值向量放在第一个位置。
2) Group向量要比freq向量多出一个长度。
3) 默认分组区间是左开右闭,如果想变为左闭右开可以设置right=FALSE。row.names可以自定义行的名称。
4) 返回的是一个数据框。特别要注意对第一列的处理。
> x=grouped.data(Group= c(0, 25, 50, 100, 150,250, 500),
Line.1 = c(30, 31, 57, 42, 65, 84),
Line.2 = c(26, 33, 31, 19, 16, 11))
> x
Group Line.1 Line.2
1 (0, 25] 30 26
2 (25, 50] 31 33
3 (50, 100] 57 31
4 (100, 150] 42 19
5 (150, 250] 65 16
6 (250, 500] 84 11
> x=grouped.data(Group= c(0, 25, 50, 100, 150,250, 500),
Line.1 = c(30, 31, 57, 42, 65, 84),
Line.2 = c(26, 33, 31, 19, 16, 11),
right=F,row.names=LETTERS[1:6])
> x
Group Line.1 Line.2
A [0, 25) 30 26
B [25, 50) 31 33
C [50, 100) 57 31
D [100, 150) 42 19
E [150, 250) 65 16
F [250, 500) 84 11
提取子总体
> x[1,]
Group Line.1 Line.2
A [0, 25) 30 26
提取组频
> x[,2]
[1] 30 31 57 42 65 84
提取边界值。如果引用第一列你期待会出现什么结果呢?
> x[,1]
[1] 0 25 50 100 150 250 500
如同任何对数据框的操作,也可以对数据框中的数据进行修改。特别需要注意的是对第一列的修改,一定要明确指定分组区间的左右(或者中间)的边界值。如:
> x[1,1]=c(0,20)
> x
Group Line.1 Line.2
1 (0, 20] 30 26
2 (20, 50] 31 33
3 (50, 100] 57 31
4 (100, 150] 42 19
5 (150, 250] 65 16
6 (250, 500] 84 11
> x[c(3, 4), 1] x
Group Line.1 Line.2
1 (0, 20] 30 26
2 (20, 55] 31 33
3 (55, 110] 57 31
4 (110, 160] 42 19
5 (160, 250] 65 16
6 (250, 500] 84 11
如果只指定一个边界的话……
> x[1,1]=10
> x
Group Line.1 Line.2
1 (10, 10] 30 26
2 (10, 55] 31 33
3 (55, 110] 57 31
4 (110, 160] 42 19
5 (160, 250] 65 16
6 (250, 500] 84 11
2、分组统计
1)函数mean()计算分组均值。等价于
$$\frac{1}{n}\sum_{j=1}^r n_j(\frac{c_{j-1}+c_j}{2})$$
高阶矩的计算可以用函数emm(),见后文。
> x
Group Line.1 Line.2
A [0, 25) 30 26
B [25, 50) 31 33
C [50, 100) 57 31
D [100, 150) 42 19
E [150, 250) 65 16
F [250, 500) 84 11
> mean(x)
Line.1 Line.2
179.81392 99.90809
Line.1的均值等价于:
> ((0+25)/2*30+(25+50)/2*31+(50+100)/2*57+(100+150)/2*42
(150+250)/2*65+(250+500)/2*84)/sum(x[,2])
[1] 179.8139
2)绘制直方图
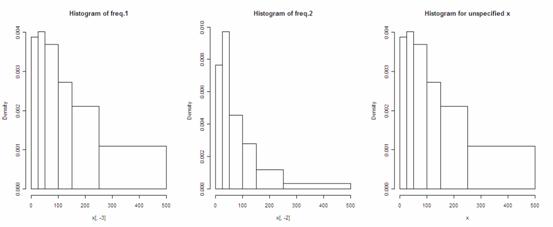
由于数据已经被划分好组别,因此R会应用数据框x的第一列作为组距的划分来绘制直方图,因此第一列一定要保留,这在绘制不等距直方图时是十分方便的。由于每次只能绘制一组频率,因此绘图时需要指定频率所在的列,如果不指定,默认绘制第一组频率(数据框的第二列)。
> layout(matrix(1:3,1,3))
> hist(x[,-3],main='Histogram of freq.1')
> hist(x[,-2],main='Histogram of freq.2')
> hist(x,main='Histogram for unspecified x')
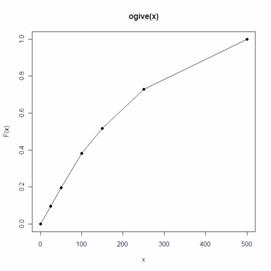
3)绘制累计频率图。如同对连续的随机变量可以绘制经验分布函数图一样,对于分组曲线也可以绘制“拱形图”(ogive),也就是累计频率曲线,它通过将分组边界值所对应的累计频率用直线连接起来得到。累计频率曲线的公式如下:
$$\tilde{F}_n(x)=\begin{cases}0 &, x\leq c_0\\\frac{(c_j-x)F_n(c_{j-1})+(x-c_{j-1})F_n(c_j)}{c_j-c_{j-1}} &, c_{j-1}<x\leq c_j\\1 &, x>c_r\\\end{cases}$$
函数ogive()返回的是一个阶梯函数对象(Step Function Class),也就是说返回的是一个函数,给定函数的横坐标,就可以返回相对应的频率,这点和ecdf()是相同的。我们可以通过konts()返回阶梯函数对象的临界点,通过plot()绘制阶梯函数。
> Fnt knots(Fnt) #返回临界点
[1] 0 25 50 100 150 250 500
> Fnt(knots(Fnt)) #返回临界点对应的累积频率值
[1] 0.00000000 0.09708738 0.19741100 0.38187702
0.51779935 0.72815534 1.00000000
> plot(Fnt)
3、计算经验矩
如果说均值函数mean()只能计算一阶矩,那么emm()函数则可以计算任意阶的经验原点矩。
首先引入actuar包中的两个数据集。其中dental是非分组数据,gdental是分组数据。
> data(dental)
> dental
[1] 141 16 46 40 351 259 317 1511 107 567
> data(gdental)
> gdental
cj nj
1 (0, 25] 30
2 ( 25, 50] 31
3 ( 50, 100] 57
4 (100, 150] 42
5 (150, 250] 65
6 (250, 500] 84
7 (500, 1000] 45
8 (1000, 1500] 10
9 (1500, 2500] 11
10 (2500, 4000] 3
emm()函数可以计算任意阶经验原点矩,其使用方法是这样的: emm(x,order=1)。其中,x可以是数据向量或者是矩阵,如果是分组数据,x也可以是由grouped.data()生成的数据框。order是阶数,可以赋值给它一个向量,这样就能一次性计算多个原点矩。
当为非分组数据时,计算的公式为:
$$\sum_{j=1}^n x_j^k$$
当为分组数据时,计算的公式为:
$$\sum_{j=1}^r n_j\frac{(c_j^{k+1}-c_{j-1}^{k+1})}{n*(k+1)*(c_j-c_{j-1})}$$
> emm(dental,2)
[1] 293068.3
> emm(gdental,1:3)
[1] 3.533399e+02 3.576802e+05 6.586332e+08
elev()函数可以计算经验有限期望值(limited expected value)。使用方法是elev(x):x可以是非分组数据,也可以是分组数据,如果是分组数据,默认以第一组频率为计算对象。
对于非分组数据,有限期望值的公式为:
$$E[X\wedge u]=f(u)=\frac{1}{n}\sum_{j=1}^n\min(x_j,u)$$
对于分组数据,有限期望公式比较复杂,在此略去。
注意到,有限期望值是上限值u的函数。
> lev=elev(dental)
> lev(knots(lev))
[1] 16.0 37.6 42.4 85.1 105.5 164.5 187.7 197.9 241.1 335.5
> lev2=elev(gdental)
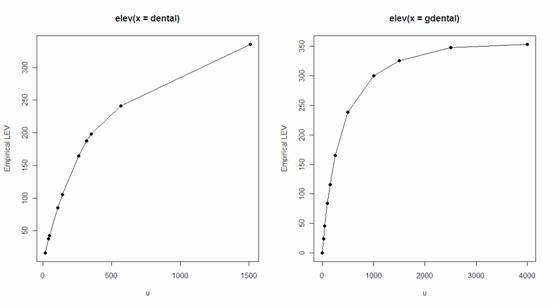
> par(mfrow=c(1,2))
> plot(lev,type='o',pch=19)
> plot(lev2,type='o',pch=19)
4、分布拟合
在R中,MASS包中的fitdistr()函数可以用极大似然估计,对数据进行分布拟合。在actuar()包中,mde()函数则提供了三种基于距离最小化的估计方法(minium distance estimates)。
1) Cramér-von Mises方法(CvM)最小化理论分布函数和经验分布函数(对于分组数据是ogive)的距离。
未分组数据:
$$d(\theta)=\sum_{j=1}^r w_j(F(x_j;\theta)-F_n(x_j))^2$$
分组数据:
$$d(\theta)=\sum_{j=1}^rw_j(F(c_j;\theta)-\tilde{F}_n(c_j))^2$$
在这里,$F(x;\theta)$是理论分布函数,$/theta$是其参数;$F_n(x)$是经验分布函数ecdf;$\tilde{F}_n(x)$是累积频率函数ogive;$w_j$是权重,默认都取1。
2)修正卡方法仅应用于分组数据,通过最小化各组期望频数与实际观测频数的平方误差得到。
$$d(\theta)=\sum_{j=1}^rw_j[n(F(c_j;\theta)-F(c_{j-1};\theta))-n_j]^2$$
其中,$n=\sum_{j=1}^nn_j$,$w_j$默认情况下为$n_j^{-1}$。
3)LAS法(layer average severity)也仅应用于分组数据。通过最小化各组内的理论和经验有限期望函数的平方误差得到。
$$d(\theta)=\sum_{j=1}^r w_j(LAS(c_{j-1},c_j;\theta)-L\tilde{A}S_n(c_{j-1},c_j))^2$$
其中$LAS(x,y)=E(X\wedge y)-E(X\wedge x)$,$L\tilde AS_n(x,y)=\tilde E_n[X\wedge y]-\tilde E_n[X\wedge x]$,$E()$是理论分布的有限期望函数,而$\tilde E_n$是经验分布的有限期望函数。$w_j$默认情况下为$n_j^{-1}$。
函数调用optim()函数做最优化,其语法为:
mde(x, fun, start, measure = c("CvM", "chi-square", "LAS"),
weights = NULL, ...)
其中:
- x是分组的或未分组的数据。
- fun是待拟合的分布,CvM法和修正卡方法需要指定分布函数:dfoo。LAS法需要指定理论有限期望函数。 Tips:R中对于一些分布foo提供了d,p,q,r四种函数,分别是密度函数,分布函数,分布函数的反函数和生成该分部的随机数。在actuar包中,除了提供R中原先没有但在精算研究中很重要的分布(比如pareto分布)的上述函数外,还对一些连续分布(注意是连续分布!)额外提供了m、lev和mgf三种函数,m是计算理论原点矩,lev是计算有限期望函数,mgf是计算矩母函数。对于经验数据,如上面介绍actuar包中提供了emm()和lev()来计算经验原点矩和经验有限期望函数。
- start指定参数初始值。形式必须以列表的形式,形式可以见例子,有几个参数就要指定几个初始值。
- measure是指定方法。weight指定权重,否则采用默认权重。
- …是其他参数,可以指定optim()函数中的参数,比如使用L-BFGS-B方法进行优化可以添加参数method=“L-BFGS-B”。
我们可以对上面的gdental数据进行分布拟合。
> mde(gdental,pexp,start=list(rate=1/200),measure="CvM")
rate
0.003551270
distance
0.002841739
Warning message:
In optim(x = c(0, 25, 50, 100, 150, 250, 500, 1000, 1500, 2500, :
one-diml optimization by Nelder-Mead is unreliable: use optimize
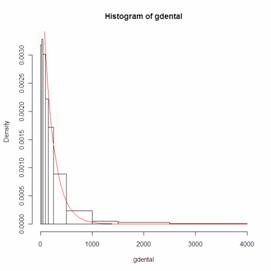
> hist(gdental)
> theta=1/200
> curve(theta*exp(1)^(-theta*x),from=0,to=4000,add=T,col='red')
 在此,我们感兴趣的是将基于距离的分布拟合方法与极大似然估计的参数估计效果进行以下对比。因此不妨做一个实验:
在此,我们感兴趣的是将基于距离的分布拟合方法与极大似然估计的参数估计效果进行以下对比。因此不妨做一个实验:
简单起见,先从单参数拟合问题开始,这是一个一维优化问题。
首先生成50组来自于rate=1的指数分布随机数,每组的个数都为10。然后,对于每一组随机数,分别用基于距离的估计方法和极大似然估计进行参数估计,将50次模拟结果的均值和标准差记录下来。之后,将随机数的个数由10增加到20,30…200,重复之前的过程。最终得到的结果如下图:
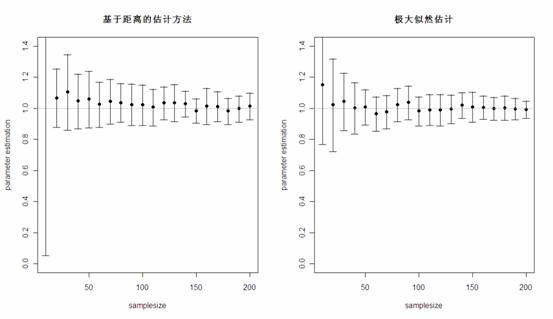
可以看出,在单参数估计中,尤其是在样本量较大时,两种方法估计的结果相差不大,而极大似然估计的方差要比基于距离的估计方差略小。那么,两种方法对于异常值的稳健性如何呢?在上面生成的所有组随机数中,剔除两个指数分布随机数,再混入两个来自[200,300]均匀分布的随机数,再重新对参数进行估计,结果很明显,基于距离的估计方法估计的结果很稳定,而极大似然估计的参数结果受异常值的影响很大!
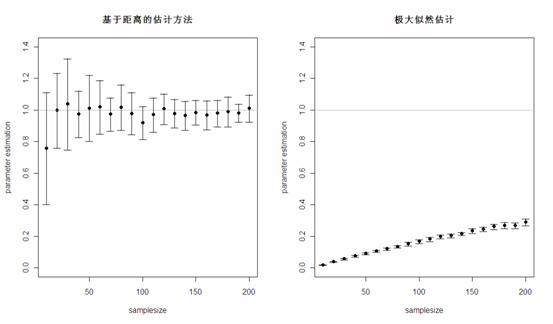
因此,对于经常存在异常值的损失数据,使用基于距离的分布拟合方法往往更加稳健。
对于两参数的估计,使用mde()函数经常会报错,通常的解决办法是估计参数的对数形式,然后再取指数还原,由于参数的对数形式可以取负值,这样程序虽然也会优化失败,但要比不取对数时的可能性要小很多。
比如:
> pgammalog=function(x,logshape,logscale)
{
pgamma(x,exp(logshape),exp(logscale))
}
>
> aa=rgamma(200,shape=3,scale=1)
> estlog=mde(aa,pgammalog,start=list(logshape=1.3,logscale=0.2),
measure='CvM',method='L-BFGS-B',lower=c(0.5,-0.5),
upper=c(1,5,0.5))$estimate
> exp(estlog)
logshape logscale
2.4873247 0.8404548
(未完待续)

发表/查看评论