
抬头,他们看到了诗云。
诗云处于已消失的太阳系所在的位置,是一片直径为一百个天文单位的旋涡状星云,形状很像银河系。空心地球处于诗云边缘,与原来太阳在银河系中的位置也很相似,不同的是地球的轨道与诗云不在同一平面,这就使得从地球上可以看到诗云的一面,而不是像银河系那样只能看到截面。
——刘慈欣 《诗云》
时光荏苒,距离上次论词已经过去了一年。今天我们接着这一话题,不过这回要看的是词牌和作者。
既然数据库里面有词牌和作者的记录,那么一个很自然的疑问是,哪些词牌被使用的频率最高?又有哪些词人的词作最为丰盛?这两个问题并不困难,只需要对他们进行频率统计然后排序即可。以下是R语言的代码和结果(数据下载地址):
doc = read.csv("SongPoem.csv");
author = doc$Author;
cipai = doc$Title2;
tab = table(author, cipai);
r1 = sort(table(author), decreasing = TRUE)[1:20];
r1 = data.frame(Author = names(r1), Freq = r1);
rownames(r1) = 1:nrow(r1);
r1
r2 = sort(table(cipai), decreasing = TRUE)[1:20];
r2 = data.frame(Cipai = names(r2), Freq = r2);
rownames(r2) = 1:nrow(r2);
r2
按作者排序(无名氏指代所有不知道姓名的作者,非特指某一位):
Author Freq
1 <无名氏> 1569
2 辛弃疾 629
3 苏轼 362
4 刘辰翁 356
5 吴文英 341
6 赵长卿 339
7 张炎 302
8 贺铸 283
9 刘克庄 269
10 晏几道 260
11 吴潜 258
12 朱敦儒 246
13 欧阳修 242
14 张孝祥 224
15 柳永 213
16 陈允平 209
17 毛滂 204
18 李曾伯 202
19 韩淲 197
20 黄庭坚 192
按词牌排序(“失调名”指词牌名已佚失,同样是很多个的集合):
Cipai Freq
1 浣溪沙 814
2 水调歌头 711
3 鹧鸪天 641
4 菩萨蛮 603
5 念奴娇 590
6 满江红 529
7 西江月 492
8 临江仙 477
9 蝶恋花 476
10 减字木兰花 441
11 贺新郎 438
12 沁园春 432
13 点绛唇 388
14 <失调名> 371
15 清平乐 346
16 满庭芳 325
17 玉楼春 308
18 水龙吟 305
19 虞美人 298
20 好事近 296
对于作者,里面有不少“熟人”,也有一些“生面孔”,看来并不是越高产的词人越能流芳后世。有时候你了解一个词人,或许只是被他/她的一首词,甚至一句话所打动,而更多的人恐怕只能是在时间的沉淀中化作历史的尘埃。这当然是题外话了。
以上的结果十分明显,也不是本文的重点,所以就不再细说了。注意到这两个排序是将词牌和作者分开来看,那我们不禁要问,词牌和作者之间是否存在一些联动的关系?比如,我们想知道是否有那么一些人,他们都喜欢用同一批词牌来作词;又或者,是否那些高产的词人经常用的也是那些高频的词牌呢?
对于这个疑问,一个很直接的想法是做出词人与词牌的对应关系。在《全宋词》的数据中,共有1377位词人和876个词牌,那么我们就可以构造一个1377*876的0-1矩阵,取1的元素表示这一行所对应的词人使用了这一列对应的词牌。我们将这个矩阵变成一张图片,每一个像素点就是矩阵的一个元素,黑色的部分是0,白色的部分是1,结果就会是下面这样:
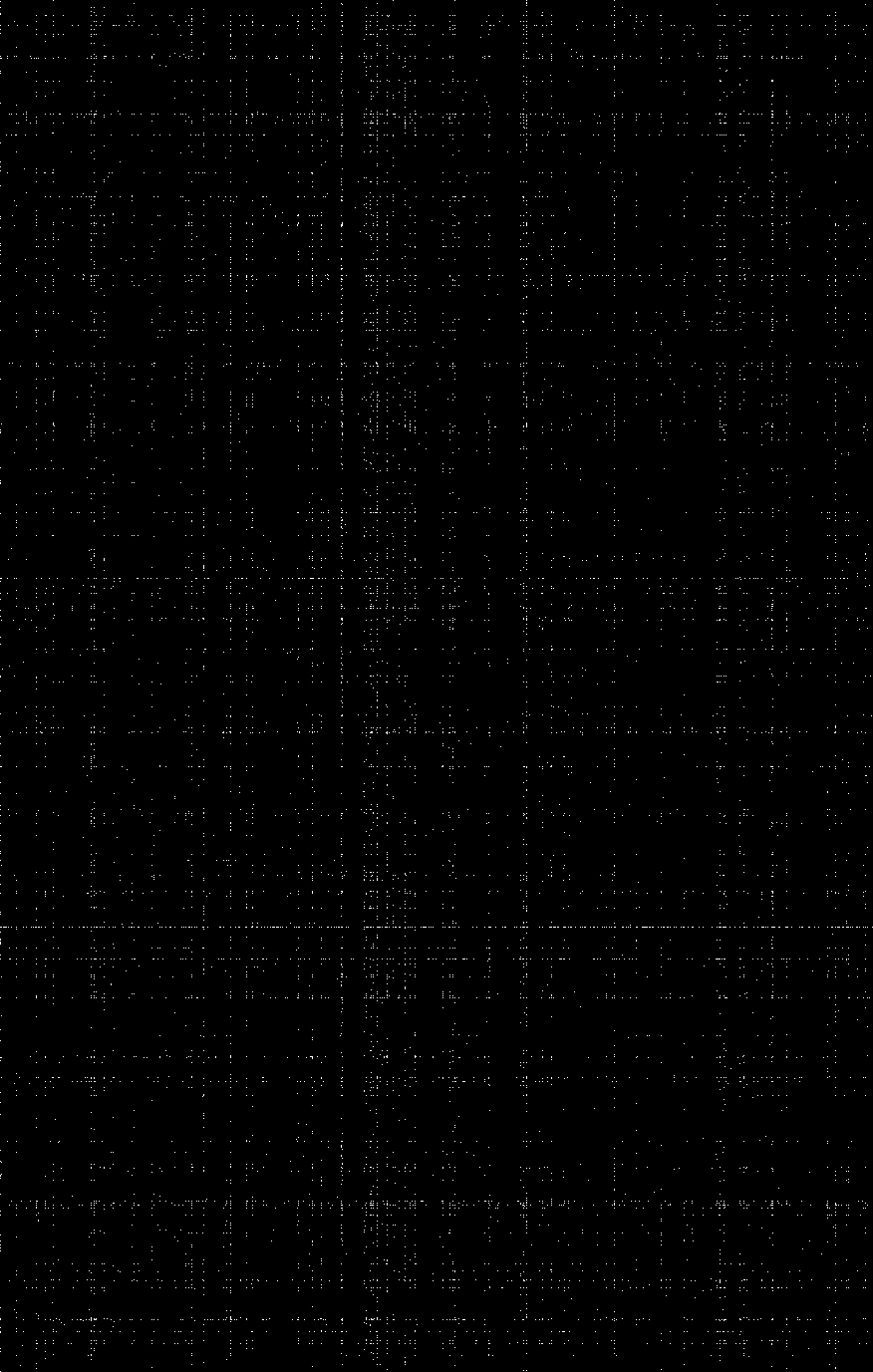
从这张“夜空中的星星”我们可以发现,绝大部分的点都被黑色所占据,这其实很容易理解:一个词人不可能写过所有的词牌,一个词牌也不可能人人都会去写。然而我们会注意到一个问题——“星星”隔得太远了。在黑色的背景中,这些“星星”零散地分布在夜空中的各个角落,而出于一种“星星相惜”的心情,我们似乎希望能把那些最亮的“星”聚在一起。
但这至少在技术上就遇到了一个问题:矩阵的每一行代表一位作者,每一列代表一个词牌,如果我们想要交换两位作者(或两个词牌)的位置,就会同时交换矩阵的某两行(或某两列),这样一来,当你拉近了某两颗“星”的距离,就可能同时延长了另外两颗“星”的距离。
为了解决这个矛盾,在此向大家介绍一种叫做双向聚类(Co-clustering,Biclustering,或Two-mode clustering)的算法。双向聚类是一种矩阵排序技术,简单地来说,它就是通过矩阵中行与行之间、列与列之间的交换,来使得取值相近的元素尽可能靠在一起,达到聚类的效果。我们使用R中的seriation软件包来对之前的0-1矩阵进行聚类,最终可以得到这样的一张图:
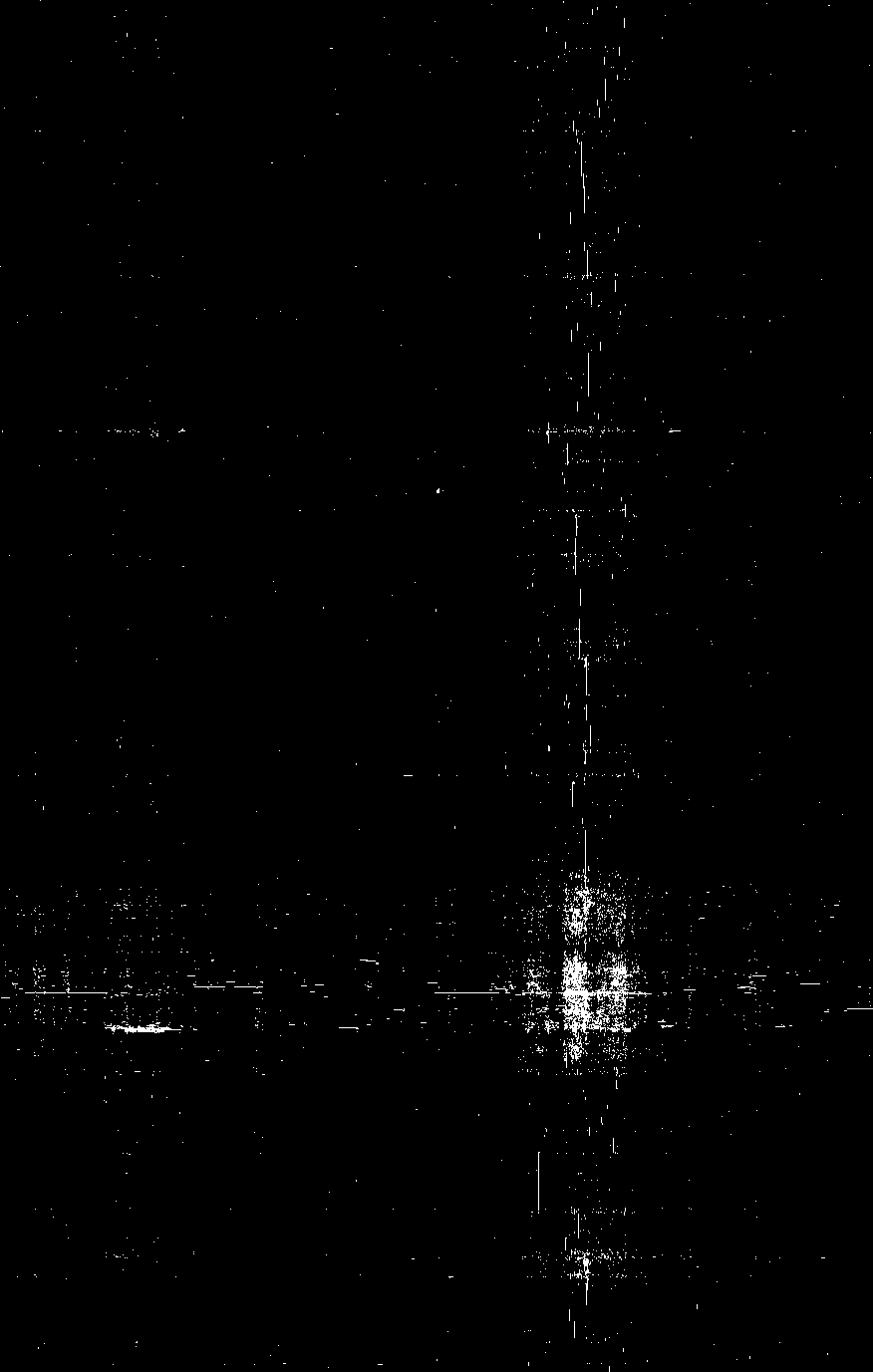
很明显,这张图中“星星”变得更加集中,放眼望去,就好像是文字和名字交织成的两条银河。让我们把目光聚焦到“星星”最密集的地方,最后可以得到以下这几个“星团”(只选取了若干最有代表性的):
| 满江红 | 念奴娇 | 水调歌头 | |
| 吴潜 | 36 | 8 | 23 |
| 刘辰翁 | 4 | 16 | 26 |
| 辛弃疾 | 34 | 22 | 38 |
| 无名氏 | 42 | 42 | 40 |
| 西江月 | 鹧鸪天 | 临江仙 | |
| 刘辰翁 | 3 | 7 | 15 |
| 辛弃疾 | 17 | 63 | 24 |
| 无名氏 | 43 | 60 | 24 |
| 赵长卿 | 3 | 21 | 16 |
| 浣溪沙 | 菩萨蛮 | 蝶恋花 | |
| 张孝祥 | 30 | 22 | 5 |
| 石孝友 | 4 | 3 | 3 |
| 朱敦儒 | 8 | 5 | |
| 黄庭坚 | 3 | 3 | 1 |
| 苏轼 | 46 | 22 | 15 |
| 陈亮 | 2 | 1 | |
| 赵彦端 | 8 | 6 | 2 |
| 韩淲 | 36 | 16 | 5 |
| 浣溪沙 | 菩萨蛮 | 蝶恋花 | 点绛唇 | |
| 辛弃疾 | 20 | 22 | 12 | 2 |
| 无名氏 | 22 | 11 | 12 | 19 |
| 赵长卿 | 21 | 17 | 9 | 12 |
| 张元干 | 16 | 8 | 3 | 10 |
| 清平乐 | 浣溪沙 | 菩萨蛮 | 蝶恋花 | |
| 欧阳修 | 1 | 9 | 22 | |
| 贺铸 | 7 | 27 | 12 | 9 |
| 毛滂 | 20 | 27 | 8 | 9 |
| 向子諲 | 7 | 25 | 4 | 2 |
矩阵中的元素表示这个词人写过多少篇对应词牌的词作。
矩阵排序在数据可视化方面还有很多有意思的应用,例如在相关矩阵可视化中,通过对相关系数矩阵进行排序,可以更清楚地看出变量之间的相关关系。以下图形来自于corrplot软件包corrMatOrder()函数的帮助文档:
par(mfrow = c(1, 2));
M = cor(mtcars);
order.AOE = corrMatOrder(M, order = "AOE");
M.AOE = M[order.AOE, order.AOE]
corrplot(M);
corrplot(M.AOE);
corrRect(c(4, 2, 5));
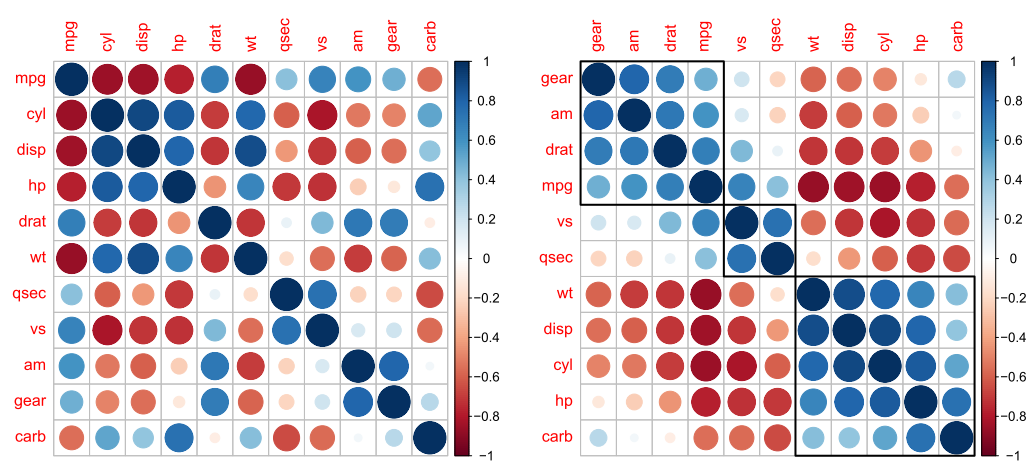
关于双向聚类只是在这里做一个简单的介绍,如果对此感兴趣,还可以继续搜索相关的文献,例如这篇综述文章。
======================开始跑题的分割线======================
你有没有觉得之前那张黑夜与星星的图不够炫?那是因为词人和词牌这两个维度是在相互垂直的坐标轴上,所以给人一种太规整的感觉。接下来我们摆弄一个小的技巧,就是把它们放到极坐标中,每一个词牌代表一个角度(方向),每一位词人则对应于一个距离,于是之前的那张图就转变成了下面的样子:

最后,我们再用核密度平滑来模拟星光的效果(使用smoothScatter()绘制平滑散点图),就成了最后这片璀璨的群星:
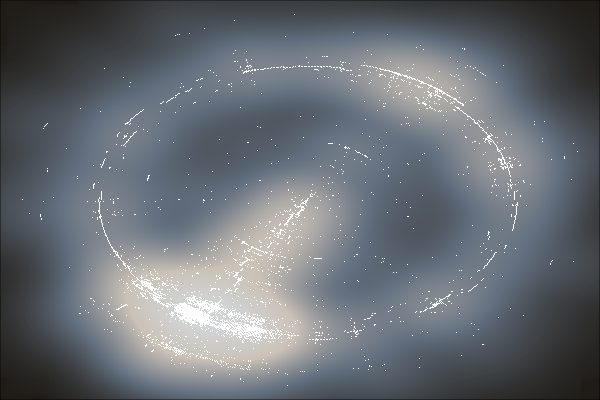
在这一片星海中,每一个同心圆(椭圆)都代表了一位词人,而从中心向外的每一个方向都是一个词牌。这是人类的群星闪耀时,而幸运的是,这一片星空,是属于这个古老的国度的。
附:绘制图形的R语言代码
visualizeMatrix = function(m)
{
m = m > 0;
par(mar = c(0, 0, 0, 0));
m = m[nrow(m):1, ];
image(1:ncol(m), 1:nrow(m), t(m), col = c("black", "white"),
useRaster = TRUE);
}
# 0-1矩阵
visualizeMatrix(tab[, ]);
# 矩阵排序
library(seriation);
set.seed(123);
ord = seriate(tab[, ] > 0);
m = permute(tab[, ], ord);
visualizeMatrix(m);
# 极坐标计算
coord = which(m > 0, arr.ind = TRUE);
theta = (coord[, 2] - 1) / (max(coord[,2 ]) - 1) * 359 / 180 * pi;
rho = coord[, 1] / max(coord[, 1]);
x = rho * cos(theta);
y = rho * sin(theta);
# 极坐标图
par(bg = "black", mar = c(0, 0, 0, 0));
plot(x, y, col = "white", pch = ".");
# 平滑散点图
par(bg = "black", mar = c(0, 0, 0, 0));
mypalette = colorRampPalette(c("#1F1C17", "#637080",
"#CBC2B7", "#D2D6D9"),
space = "Lab");
smoothScatter(x, y, colramp = mypalette, nbin = 600, bandwidth = 0.1,
col = "white", nrpoints = Inf);


发表/查看评论