4. 文本建模

我们日常生活中总是产生大量的文本，如果每一个文本存储为一篇文档，那每篇文档从人的观察来说就是有序的词的序列$d=(w_1, w_2, \cdots, w_n)$。

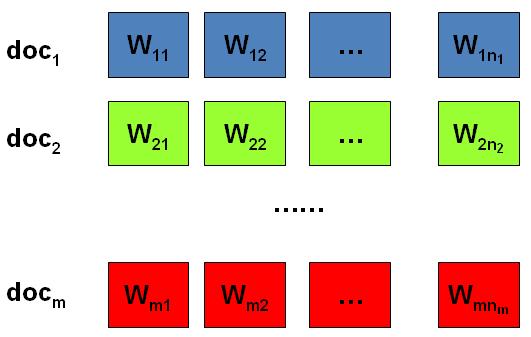包含$M$篇文档的语料库

统计文本建模的目的就是追问这些观察到语料库中的的词序列是如何生成的。统计学被人们描述为猜测上帝的游戏，人类产生的所有的语料文本我们都可以看成是一个伟大的上帝在天堂中抛掷骰子生成的，我们观察到的只是上帝玩这个游戏的结果 —— 词序列构成的语料，而上帝玩这个游戏的过程对我们是个黑盒子。所以在统计文本建模中，我们希望猜测出上帝是如何玩这个游戏的，具体一点，最核心的两个问题是

• 上帝都有什么样的骰子；
• 上帝是如何抛掷这些骰子的；

第一个问题就是表示模型中都有哪些参数，骰子的每一个面的概率都对应于模型中的参数；第二个问题就表示游戏规则是什么，上帝可能有各种不同类型的骰子，上帝可以按照一定的规则抛掷这些骰子从而产生词序列。

上帝掷骰子

4.1 Unigram Model

假设我们的词典中一共有$V$个词$v_1, v_2, \cdots v_V$，那么最简单的 Unigram Model 就是认为上帝是按照如下的游戏规则产生文本的。

上帝的这个唯一的骰子各个面的概率记为$\overrightarrow{p} = (p_1, p_2, \cdots, p_V)$， 所以每次投掷骰子类似于一个抛钢镚时候的贝努利实验， 记为$w\sim Mult(w|\overrightarrow{p})$。

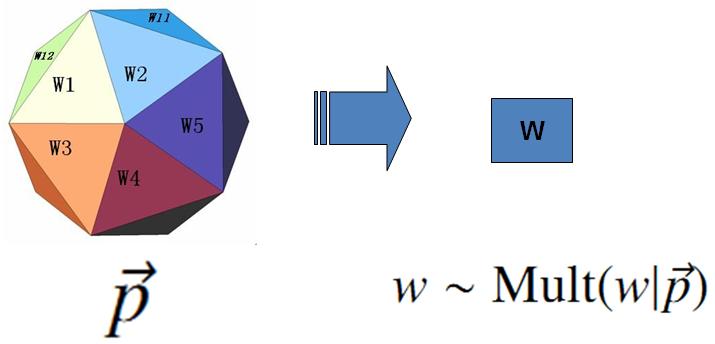
上帝投掷$V$个面的骰子

对于一篇文档$d=\overrightarrow{w}=(w_1, w_2, \cdots, w_n)$， 该文档被生成的概率就是

$$ p(\overrightarrow{w}) = p(w_1, w_2, \cdots, w_n) = p(w_1)p(w_2) \cdots p(w_n) $$

而文档和文档之间我们认为是独立的，所以如果语料中有多篇文档$\mathcal{W}=(\overrightarrow{w_1}, \overrightarrow{w_2},…,\overrightarrow{w_m})$，则该语料的概率是

$$p(\mathcal{W})= p(\overrightarrow{w_1})p(\overrightarrow{w_2})\cdots p(\overrightarrow{w_m}) $$

在 Unigram Model 中， 我们假设了文档之间是独立可交换的，而文档中的词也是独立可交换的，所以一篇文档相当于一个袋子，里面装了一些词，而词的顺序信息就无关紧要了，这样的模型也称为词袋模型(Bag-of-words)。

假设语料中总的词频是$N$， 在所有的$N$个词中,如果我们关注每个词$v_i$的发生次数$n_i$，那么 $\overrightarrow{n}=(n_1, n_2,\cdots, n_V)$正好是一个多项分布

$$ p(\overrightarrow{n}) = Mult(\overrightarrow{n}|\overrightarrow{p}, N) = \binom{N}{\overrightarrow{n}} \prod_{k=1}^V p_k^{n_k} $$

此时， 语料的概率是

\begin{align*} p(\mathcal{W})= p(\overrightarrow{w_1})p(\overrightarrow{w_2}) \cdots p(\overrightarrow{w_m}) = \prod_{k=1}^V p_k^{n_k} \end{align*}

当然，我们很重要的一个任务就是估计模型中的参数$\overrightarrow{p}$，也就是问上帝拥有的这个骰子的各个面的概率是多大，按照统计学家中频率派的观点，使用最大似然估计最大化$P(\mathcal{W})$，于是参数$p_i$的估计值就是

$$ \hat{p_i} = \frac{n_i}{N} .$$

对于以上模型，贝叶斯统计学派的统计学家会有不同意见，他们会很挑剔的批评只假设上帝拥有唯一一个固定的骰子是不合理的。在贝叶斯学派看来，一切参数都是随机变量，以上模型中的骰子 $\overrightarrow{p}$不是唯一固定的，它也是一个随机变量。所以按照贝叶斯学派的观点，上帝是按照以下的过程在玩游戏的

上帝的这个坛子里面，骰子可以是无穷多个，有些类型的骰子数量多，有些类型的骰子少，所以从概率分布的角度看，坛子里面的骰子$\overrightarrow{p}$服从一个概率分布$p(\overrightarrow{p})$，这个分布称为参数$\overrightarrow{p}$的先验分布。

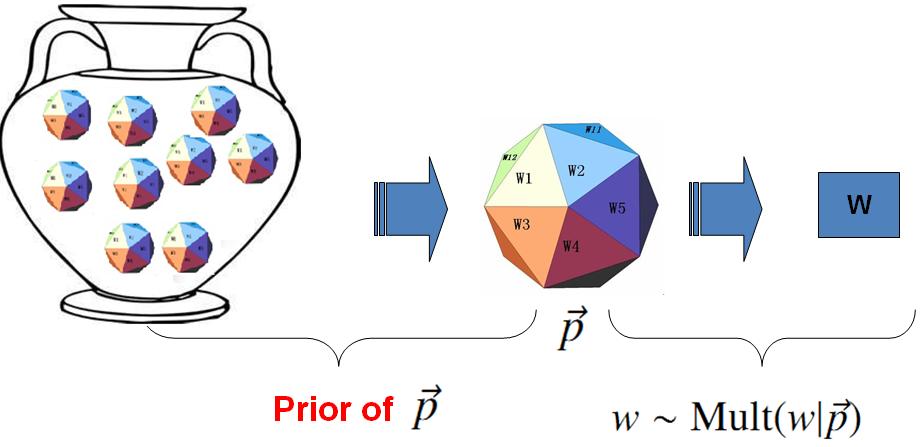
贝叶斯观点下的 Unigram Model

以上贝叶斯学派的游戏规则的假设之下，语料$\mathcal{W}$产生的概率如何计算呢？由于我们并不知道上帝到底用了哪个骰子$\overrightarrow{p}$，所以每个骰子都是可能被使用的，只是使用的概率由先验分布$p(\overrightarrow{p})$来决定。对每一个具体的骰子$\overrightarrow{p}$，由该骰子产生数据的概率是$p(\mathcal{W}|\overrightarrow{p})$， 所以最终数据产生的概率就是对每一个骰子$\overrightarrow{p}$上产生的数据概率进行积分累加求和

$$ p(\mathcal{W}) = \int p(\mathcal{W}|\overrightarrow{p}) p(\overrightarrow{p})d\overrightarrow{p} $$

在贝叶斯分析的框架下，此处先验分布$p(\overrightarrow{p})$就可以有很多种选择了，注意到

$$ p(\overrightarrow{n}) = Mult(\overrightarrow{n}|\overrightarrow{p}, N) $$

实际上是在计算一个多项分布的概率，所以对先验分布的一个比较好的选择就是多项分布对应的共轭分布，即 Dirichlet 分布

$$ Dir(\overrightarrow{p}|\overrightarrow{\alpha})= \frac{1}{\Delta(\overrightarrow{\alpha})} \prod_{k=1}^V p_k^{\alpha_k -1}，\quad \overrightarrow{\alpha}=(\alpha_1, \cdots, \alpha_V) $$

此处，$\Delta(\overrightarrow{\alpha})$就是归一化因子$Dir(\overrightarrow{\alpha})$，即

$$ \Delta(\overrightarrow{\alpha}) = \int \prod_{k=1}^V p_k^{\alpha_k -1} d\overrightarrow{p} . $$

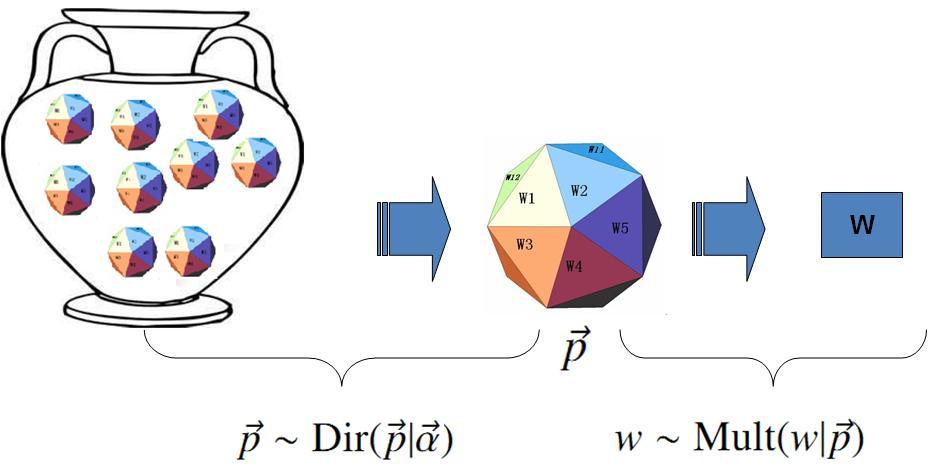
Dirichlet 先验下的 Unigram Model

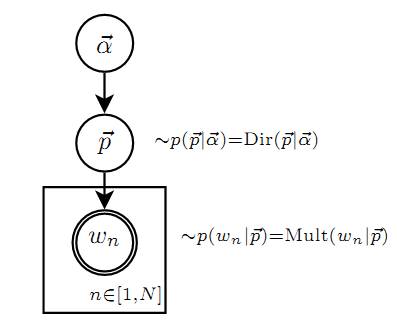
Unigram Model的概率图模型

回顾前一个小节介绍的 Drichlet 分布的一些知识，其中很重要的一点就是

Dirichlet 先验 + 多项分布的数据$\rightarrow$后验分布为 Dirichlet 分布

$$ Dir(\overrightarrow{p}|\overrightarrow{\alpha}) + MultCount(\overrightarrow{n})= Dir(\overrightarrow{p}|\overrightarrow{\alpha}+\overrightarrow{n}) $$

于是，在给定了参数$\overrightarrow{p}$的先验分布$Dir(\overrightarrow{p}|\overrightarrow{\alpha})$的时候，各个词出现频次的数据$\overrightarrow{n} \sim Mult(\overrightarrow{n}|\overrightarrow{p},N)$为多项分布, 所以无需计算，我们就可以推出后验分布是

\begin{equation} p(\overrightarrow{p}|\mathcal{W},\overrightarrow{\alpha}) = Dir(\overrightarrow{p}|\overrightarrow{n}+ \overrightarrow{\alpha}) = \frac{1}{\Delta(\overrightarrow{n}+\overrightarrow{\alpha})} \prod_{k=1}^V p_k^{n_k + \alpha_k -1} d\overrightarrow{p} \end{equation}

在贝叶斯的框架下，参数$\overrightarrow{p}$如何估计呢？由于我们已经有了参数的后验分布，所以合理的方式是使用后验分布的极大值点，或者是参数在后验分布下的平均值。在该文档中，我们取平均值作为参数的估计值。使用上个小节中的结论，由于 $\overrightarrow{p}$的后验分布为$Dir(\overrightarrow{p}|\overrightarrow{n} + \overrightarrow{\alpha})$，于是

$$ E(\overrightarrow{p}) = \Bigl(\frac{n_1 + \alpha_1}{\sum_{i=1}^V(n_i + \alpha_i)}, \frac{n_2 + \alpha_2}{\sum_{i=1}^V(n_i + \alpha_i)}, \cdots, \frac{n_V + \alpha_V}{\sum_{i=1}^V(n_i + \alpha_i)} \Bigr) $$

也就是说对每一个$p_i$， 我们用下式做参数估计

\begin{equation} \label{dirichlet-parameter-estimation} \hat{p_i} = \frac{n_i + \alpha_i}{\sum_{i=1}^V(n_i + \alpha_i)} \end{equation}

考虑到$\alpha_i$在 Dirichlet 分布中的物理意义是事件的先验的伪计数，这个估计式子的含义是很直观的：每个参数的估计值是其对应事件的先验的伪计数和数据中的计数的和在整体计数中的比例。

进一步，我们可以计算出文本语料的产生概率为

\begin{align} p(\mathcal{W}|\overrightarrow{\alpha}) & = \int p(\mathcal{W}|\overrightarrow{p}) p(\overrightarrow{p}|\overrightarrow{\alpha})d\overrightarrow{p} \notag \\ & = \int \prod_{k=1}^V p_k^{n_k} Dir(\overrightarrow{p}|\overrightarrow{\alpha}) d\overrightarrow{p} \notag \\ & = \int \prod_{k=1}^V p_k^{n_k} \frac{1}{\Delta(\overrightarrow{\alpha})} \prod_{k=1}^V p_k^{\alpha_k -1} d\overrightarrow{p} \notag \\ & = \frac{1}{\Delta(\overrightarrow{\alpha})} \int \prod_{k=1}^V p_k^{n_k + \alpha_k -1} d\overrightarrow{p} \notag \\ & = \frac{\Delta(\overrightarrow{n}+\overrightarrow{\alpha})}{\Delta(\overrightarrow{\alpha})} \label{likelihood-dir-mult} \end{align}

4.2 Topic Model 和 PLSA

以上 Unigram Model 是一个很简单的模型，模型中的假设看起来过于简单，和人类写文章产生每一个词的过程差距比较大，有没有更好的模型呢？

我们可以看看日常生活中人是如何构思文章的。如果我们要写一篇文章，往往是先确定要写哪几个主题。譬如构思一篇自然语言处理相关的文章，可能 40% 会谈论语言学、30% 谈论概率统计、20% 谈论计算机、还有10%谈论其它的主题：

• 说到语言学，我们容易想到的词包括：语法、句子、乔姆斯基、句法分析、主语…；
• 谈论概率统计，我们容易想到以下一些词: 概率、模型、均值、方差、证明、独立、马尔科夫链、…；
• 谈论计算机，我们容易想到的词是： 内存、硬盘、编程、二进制、对象、算法、复杂度…；

我们之所以能马上想到这些词，是因为这些词在对应的主题下出现的概率很高。我们可以很自然的看到，一篇文章通常是由多个主题构成的、而每一个主题大概可以用与该主题相关的频率最高的一些词来描述。

以上这种直观的想法由Hoffman 于 1999 年给出的PLSA(Probabilistic Latent Semantic Analysis) 模型中首先进行了明确的数学化。Hoffman 认为一篇文档(Document) 可以由多个主题(Topic) 混合而成， 而每个Topic 都是词汇上的概率分布，文章中的每个词都是由一个固定的 Topic 生成的。下图是英语中几个Topic 的例子。

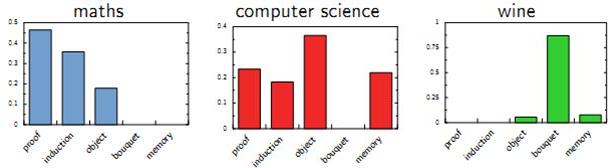
就是Vocab 上的概率分布

所有人类思考和写文章的行为都可以认为是上帝的行为，我们继续回到上帝的假设中，那么在 PLSA 模型中，Hoffman 认为上帝是按照如下的游戏规则来生成文本的。

以上PLSA 模型的文档生成的过程可以图形化的表示为

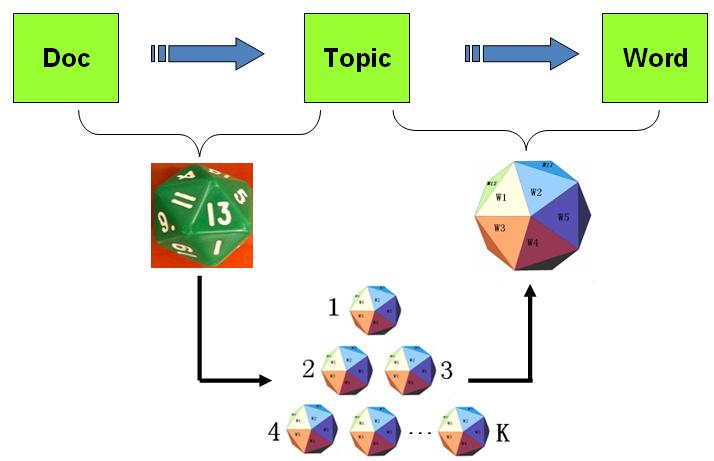
PLSA模型的文档生成过程

我们可以发现在以上的游戏规则下，文档和文档之间是独立可交换的，同一个文档内的词也是独立可交换的，还是一个 bag-of-words 模型。游戏中的$K$个topic-word 骰子，我们可以记为$\overrightarrow{\varphi}_1, \cdots, \overrightarrow{\varphi}_K$， 对于包含$M$篇文档的语料$C=(d_1, d_2, \cdots, d_M)$中的每篇文档$d_m$，都会有一个特定的doc-topic骰子$\overrightarrow{\theta}_m$，所有对应的骰子记为 $\overrightarrow{\theta}_1, \cdots, \overrightarrow{\theta}_M$。为了方便，我们假设每个词$w$都是一个编号，对应到topic-word 骰子的面。于是在 PLSA 这个模型中，第$m$篇文档$d_m$中的每个词的生成概率为

$$ p(w|d_m) = \sum_{z=1}^K p(w|z)p(z|d_m) = \sum_{z=1}^K \varphi_{zw} \theta_{mz}$$

所以整篇文档的生成概率为

$$ p(\overrightarrow{w}|d_m) = \prod_{i=1}^n \sum_{z=1}^K p(w_i|z)p(z|d_m) = \prod_{i=1}^n \sum_{z=1}^K \varphi_{zw_i} \theta_{dz} $$

由于文档之间相互独立，我们也容易写出整个语料的生成概率。求解PLSA 这个 Topic Model 的过程汇总，模型参数并容易求解，可以使用著名的 EM 算法进行求得局部最优解，由于该模型的求解并不是本文的介绍要点，有兴趣的同学参考 Hoffman 的原始论文，此处略去不讲。