微博名人那些事儿（二）

如何评价一个名人的热度？自然而然能想到的方法是，通过粉丝/关注比来评判其“风云”程度（好吧如果不考虑僵尸粉这种特色产物……><）。但实际上，在social network里面，我们真正面临的，是一个“网络”结构。让我们想想，消息在SNS里是怎么传播的呢？关注、粉丝、转发、评论 blablabla……所以，最近我在想，能不能利用这些关系来评判一个人的影响力？

首先面临的问题是，应该用什么样的行为表示人与人之间的关系呢？鉴于想对用户兴趣做一些扩展的探索，我首选了“转发”关系。而且，退一步讲，在新浪在7月2号对API做了调整限制后，关注关系及粉丝关系等就不是我们这种ds小市民那么容易得到的了。（实际上即使能够得到，我个人也认为转发关系是在信息传播力上极为重要的一环）

then，转发关系的获得只需要我们对文本做一些简单的提取、筛选工作（相比起抓数据这种偷偷摸摸的事儿文本处理真是幸福太多了我会乱说……><），代码如下（原始数据仍为《微博名人那些事儿》中的数据）：

get.retweet <-function(x,name,set=name1)
{
 weibos=c(x$Weibo,x$Forward)
 weibos=weibos[!is.na(weibos)]
 ind=gregexpr("@[\u4e00-\u9fa5\\w]+[\\s:]",weibos,perl=T)
 people=lapply(1:length(weibos),function(i) {
 if(all(ind[[i]]==-1)) return(NULL)
 return(substring(weibos[i],ind[[i]]+1,ind[[i]]+attr(ind[[i]],"match.length")-2))
 })

 pp=unlist(people)
 pp=pp[pp!=name]
 pp1=pp[is.element(pp,name1)]
 return(list(name=pp,freq=table(pp1)))
}

retweet=lapply(1:length(wei),function(i) return(get.retweet(wei[[i]],name1[i])))

retweet_name=unlist(lapply(retweet,function(x){
 return(x$name)
}))
retweet_weight=lapply(retweet,function(x) return(x$freq))

变量名称不用细究，wei存放的就是用Rweibo中web.user_timeline()函数得到的结果，name1是对应于这些结果的名人昵称。此处保存的结果为转发者对应的被转发者姓名retweet_name以及对应的转发次数retweet_weight。

有了单纯的转发关系还不够。如何利用这种关系来表征一个人的消息传播力呢？一个比较自然的想法就是Google著名的pagerank算法。根据Perron-Frobenius定理，有限状态马氏链的状态转移矩阵的特征值的模是小于等于1的。（简单的proof：马氏链的转移矩阵行之和为1，可以构造每个分量均为1的向量作为其特征向量，它对应的特征值正是实数值1；套用P-F定理既得结果）这个结果下面会用到。

正如我们所知，一条微博不会无限长的转发下去。也就是说，一条消息在每一次转发之后都可能面临着“停止传播”的命运。设这种传播停止的概率参数为d。就得到了pagerank算法的表达形式以及解析解。实际上，在这个过程中，0<d<1的约束保证了dM特征值的模小于1，因此I-dM的逆存在。这意味着存在唯一的平稳分布（也就是我们要求的PR值）使之成立。

还有一个问题是，如果一个节点的出度是0，那么对应矩阵的列元素不就全部是0了嘛？这显然不符合PR算法中列元素之和为1的要求呀。一个简单的处理方法是对这列元素都赋1/N，即认为他以相同的概率转发该网络图中所有人的微博。取d=0.85（wiki），转发关系采用稀疏矩阵方式存储，PR值计算过程如下：

get.ijv <-function(i,weight,name)
{
 if(length(weight)==0) return(NULL)
 j=which(is.element(names(weight),name))
 ijv=data.frame(i=i,j=j,v=weight)
 return(ijv)
}

ijv=do.call(rbind,lapply(1:length(retweet_weight),
 function(i) return(get.ijv(i,retweet_weight[[i]],retweet_name))))
library(Matrix)

ijv_mat=t(sparseMatrix(i=ijv[,1],j=ijv[,2],x=ijv[,4],
 dims=c(length(retweet_weight),length(retweet_weight))))

get.L<-function(v,i)
{
 if(all(v==0)) return(1/length(v))
 return(v/sum(v))
}

ijv_mat_std=do.call(cbind,lapply(1:ncol(ijv_mat),function(i) return(get.L(ijv_mat[,i],i))))

d=0.85

inverse=solve(diag(nrow(ijv_mat_std))-d*ijv_mat_std)
PR=(1-d)/nrow(ijv_mat_std)*inverse%*%matrix(1,nrow=nrow(ijv_mat_std))
names(PR)=name1
sort(PR,decreasing=T)[1:10]

结果如下：

除了网络的结构（structure），是否微博的文本信息也能被我们利用呢？例如，***和###都是体育爱好者，那么他们之间是否存在关联路径呢？如果存在，如何表示这种关系？

鉴于上一篇的结果，我们可以将人与人之间的关系用topic联系起来。在一种更广泛的定义上，除了以人作为节点（structure vertice）表征的图模型，我们还可以加入以topic作为节点的关系表示（attribute vertice）。由于增加了图的表示信息，我们将它称为“增强图”（augmented graph）【此处翻译仅为本人理解而已，这种做法在paper中比较常见】。从另一种意义上说，信息通过他与其他人的文本信息关联传播了出去。将augmented graph用矩阵形式表示出来得到：

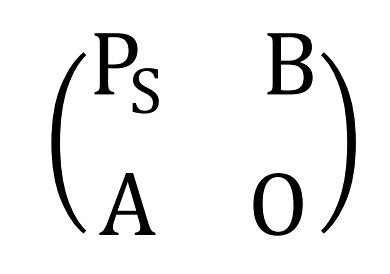
设structure vertice与attribute vertice组合的权重分别为\(\alpha\)和\(\beta\)，满足\(\alpha+\beta=1\)，即将pagerank算法中的M矩阵乘以\(\alpha\)，将topicmodel得到的topic在doc上的后验分布乘以\(\beta\)得到上述矩阵中的\(P_s\)矩阵和A矩阵。O分块矩阵为零矩阵，代表topic之间不可相互转移（实际上这个假设略强）。同时，设topic在doc上的后验分布为C（doc-topic矩阵），其每一行和为1，对其列做归一化处理可得到B矩阵。

同时，structure vertice与attribute vertice之间的区别还在于转移概率的不同。这里假设structure->structure的d参数为\(d_1\)，由structure->attribute的d参数为\(d_2\)，为了满足PR值和为1的假设，可以计算得到由attribute->structure的d参数为\(d_{1}\times\alpha+d_{2}\times\beta\)；原来的常数列则为前\(N_s\)个分量为\((1-d_1)/\alpha/{N_s}\)，后\(N_a\)个分量分别为\((1-d_2)/\beta/{N_a}\)，\(N_s\)与\(N_a\)分别表示structure vertice与attribute vertice的个数。

其数学表达式如下：

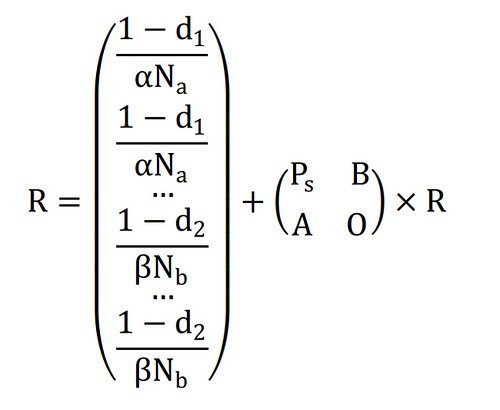
这部分代码如下：

topic_person=posterior(Gibbs_weibo,newdata=dtm)[[2]][ll,]

d1=0.85; d2=0.6
alpha=0.5; beta=0.5

ijv_mat_std1=do.call(cbind,lapply(1:ncol(ijv_mat),function(i) return(get.L(ijv_mat[,i],i))))
aug_mat=rbind(cbind(as.matrix(ijv_mat_std1),topic_person),t(rbind(topic_person,matrix(0,nrow=50,ncol=50))))

aug_mat1=do.call(cbind,lapply(1:ncol(aug_mat),function(i) return(get.L(aug_mat[,i],i))))
M=aug_mat1
M[1:334,1:334]=d1*aug_mat1[1:334,1:334]
M[335:384,1:334]=d2*aug_mat1[335:384,1:334]
M[1:334,335:384]=(d1*alpha+d2*beta)*aug_mat1[1:334,335:384]

inverse=solve(diag(nrow(aug_mat1))-M)
PR=inverse%*%matrix(c(rep((1-d1)/334/2,334),rep((1-d2)/50/2,50)),ncol=1)
names(PR)=c(name1,1:50)
sort(PR,decreasing=T)[1:10]

结果如下：

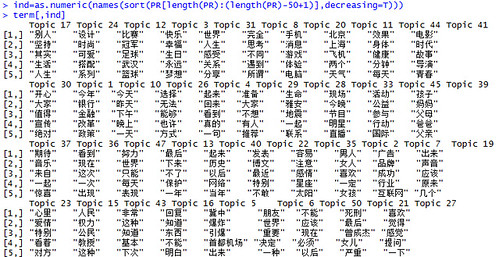
来单独看看topic的排名以及对应的高频词吧：

term=terms(Gibbs_weibo,5)
ind=as.numeric(names(sort(PR[length(PR):(length(PR)-50+1)],decreasing=T)))
term[,ind]

参考文献：

Graph Clustering Based on Structural/Attribute Similarities

Notes on PageRank Algorithm

备注

原文链接：微博名人那些事儿（二） ，转载请注明出处。