**【COS编辑部按】**本文选自狗熊会分析报告，作者为刘钰、毛铮、谯谦、吕俊杰、祁自帅、刘哲

狗熊会简介：北京大学商务智能研究中心下的的数据分析人才联盟，每周一熊出没，举报研讨会议。其依托北京大学光华管理学院，关注基于互联网的大数据研究与应用。尤其关注中文文本、网络结构、以及位置数据相关的科研课题。中心为学者提供相关数据资源，为企业提供相关分析方法，为学者和企业合作搭建一个有效的平台。

联系方式：birc@gsm.pku.ed.cn

狗熊会：有限的数据，一丁点发现，无穷多可能的解释，不知对错！但是，这不妨碍好奇与探索，以及数据分析的快乐……

摘要

新产品扩散模型是管理学研究分支，并且多以票房收入为研究素材，关注电影上映后票房的增长扩散速度。本案例通过对北美100部大片进行统计分析，发现了一个神奇的ln(t)定律。

背景介绍

电影大片的票房跟剧本、导演、演员、特效、前期的广告宣传和观众的口碑都有着密切的联系，因此预测一部电影的票房并不容易。但我们想挑战的是，如果我们知道上映第一、二天的票房，能否估算出它今后的票房呢？要回答这个问题，就需要对票房收入的扩散行为予以建模分析。

数据描述

为此，我们以上映后30天的本土票房为参考标准，选取2000-2012年间在美国本土上映的最卖座的100部电影进行统计分析。这些电影的票房更多受电影本身和观众的口碑影响更多，受同档期其他电影影响较小，我们分析起来也相对简单一些。我们从www.boxofficemojo.com网站提取了这100部电影上映后30天里每天的累计票房作为数据源进行分析。数据如下图所示

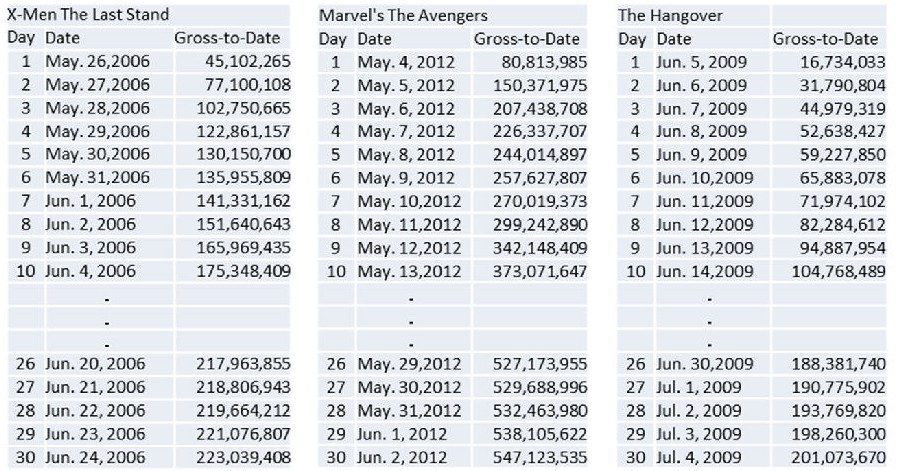
从这3个例子中，我们看到，即便都是最卖座的大片，30天的累计票房也不尽相同，而且他们的累计票房数据都呈现出非线性特征，请见下图。

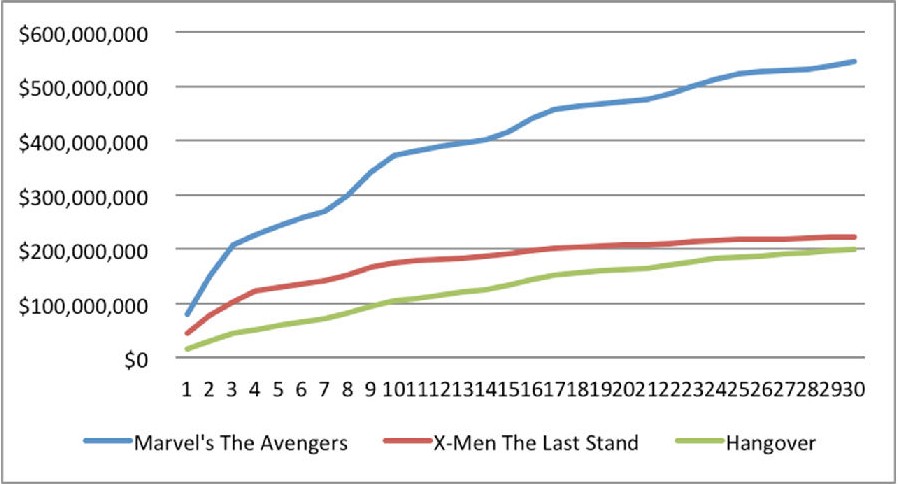
由此可见，票房的累积增加，同时间不是一个简单的线性关系。这同经典的新产品扩散理论也一致。因此，对于该数据，我们不便于直接利用线性回归方法进行分析和预测。因此，我们需要用模型转换的方法把票房数据线性化，并进行Rsq及系数统计显著性的分析。

探索性分析

作为一个探索性分析，我们从这100部电影的数据出发，而不是从理论推导开始，分别用线性函数、指数函数、对数函数、多项式函数和抛物线函数对数据进行测试，选出最契合数据本身的函数模型。最终选取了对数函数模型：N（t）= βln(t) + c ，其中t为上映的天数（首映日为t=1），N（t）为从上映以来第t天的累计票房，ln(t)为t天的自然对数，β和c是我们需要确定的系数和常数。请见下图。对比下图与上图，我们可以看到极好的线性关系。

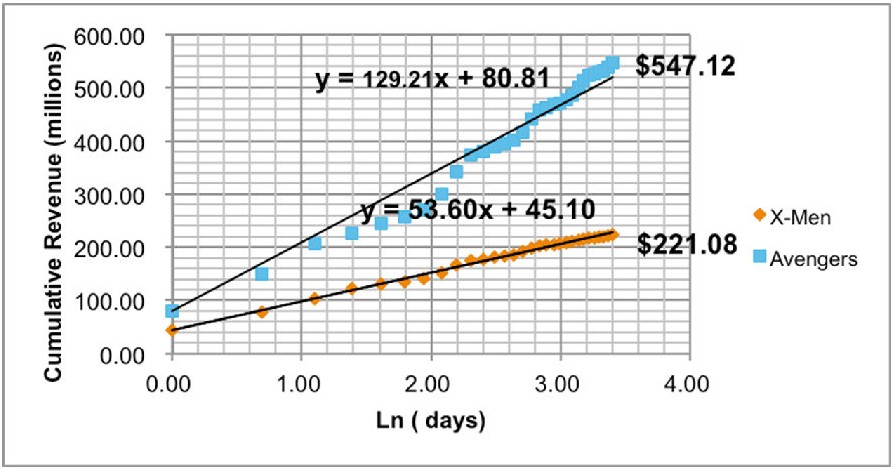
对该模型，我们简单解读如下。当t=1是，ln(t)=0,因此N（1）=c, 也就是说，在这个公式中，常数c是首映式当天的票房。到此为止，我们的数据中有了每天的累计票房N（t）, 上映天数t和首映式票房c, 可以开始检测此对数模型对数据的契合度，利用线性回归找到R2和系数β，及其统计显著性。在对这100部电影的样本分别进行线性回归的分析后，我们R2的数值均在0.8以上，有些甚至高达0.95以上，说明回归拟合的效果非常好，此模型的精确度也很高。其中我们得出每部电影的β值，其p值非常小，说明β的统计显著性也很好，进一步说明累计票房和上映天数的自然对数存在线性关系。其中票房排名前10的北美大片的分析结果如下：

基于该模型，我们尝试用前两天的票房数据预测未来的票房。经测试，在这100部电影样本中，我们测试的误差平均值为35%，在置信度为95%的水平下其置信区间为28%～36%，其中有30部电影的误差在20%以内。

总结讨论

对比对我们的预测结果与实际票房的观察，我们发现此模型对大片的续集或者内容已经被大众熟知的电影的预测准确度较高，但会大幅低估黑马电影或动画片的票房。我们分析其原因可能是我们的模型并没有对电影上映后的口碑效应进行考虑。比如阿凡达，口碑效应让其电影票房衰减速度减缓很多，因此我们的模型并没有很好地预测这一类电影的累计票房。下一步我们可以用新近上映的电影作为样本外的数据对我们的模型进行进一步的检测以避免过分的数据挖掘。并且可以结合老师上课提到的用谷歌关键词搜索的数据作为对口碑效应的预测，以完善我们的预测模型。

本案例最大的两个局限如下。第一、这是一个有趣但是非常粗糙的探索性研究，发现了神奇的ln(t)定律，但是无力解释背后的原因。第二、从票房预测而言，必须利用电影已经上映后头两天的数据进行预测。而对于最该预测的，那些还没有上映的电影无能为力。