支持向量机系列一: Maximum Margin Classifier

原文链接请点击这里

支持向量机即 Support Vector Machine，简称 SVM 。我最开始听说这头机器的名号的时候，一种神秘感就油然而生，似乎把 Support 这么一个具体的动作和 Vector 这么一个抽象的概念拼到一起，然后再做成一个 Machine ，一听就很玄了！

不过后来我才知道，原来 SVM 它并不是一头机器，而是一种算法，或者，确切地说，是一类算法，当然，这样抠字眼的话就没完没了了，比如，我说 SVM 实际上是一个分类器 (Classifier) ，但是其实也是有用 SVM 来做回归 (Regression) 的。所以，这种字眼就先不管了，还是从分类器说起吧。

SVM 一直被认为是效果最好的现成可用的分类算法之一（其实有很多人都相信，“之一”是可以去掉的）。这里“现成可用”其实是很重要的，因为一直以来学术界和工业界甚至只是学术界里做理论的和做应用的之间，都有一种“鸿沟”，有些很 fancy 或者很复杂的算法，在抽象出来的模型里很完美，然而在实际问题上却显得很脆弱，效果很差甚至完全 fail 。而 SVM 则正好是一个特例——在两边都混得开。

好了，由于 SVM 的故事本身就很长，所以废话就先只说这么多了，直接入题吧。当然，说是入贴，但是也不能一上来就是 SVM ，而是必须要从线性分类器开始讲。这里我们考虑的是一个两类的分类问题，数据点用 \(x\) 来表示，这是一个 \(n\) 维向量，而类别用 \(y\) 来表示，可以取 1 或者 -1 ，分别代表两个不同的类（有些地方会选 0 和 1 ，当然其实分类问题选什么都无所谓，只要是两个不同的数字即可，不过这里选择 +1 和 -1 是为了方便 SVM 的推导，后面就会明了了）。一个线性分类器就是要在 \(n\) 维的数据空间中找到一个超平面，其方程可以表示为

$$w^Tx + b = 0$$

一个超平面，在二维空间中的例子就是一条直线。我们希望的是，通过这个超平面可以把两类数据分隔开来，比如，在超平面一边的数据点所对应的\(y\)全是 -1 ，而在另一边全是1。具体来说，我们令 \(f(x) = w^{T}x + b\) ，显然，如果 \(f(x) = 0\) ，那么\(x\)是位于超平面上的点。我们不妨要求对于所有满足 \(f(x) < 0\)的点，其对应的\(y\)等于 -1 ，而\(f(x) > 0\)则对应 \(y = 1\) 的数据点。当然，有些时候（或者说大部分时候）数据并不是线性可分的，这个时候满足这样条件的超平面就根本不存在，不过关于如何处理这样的问题我们后面会讲，这里先从最简单的情形开始推导，就假设数据都是线性可分的，亦即这样的超平面是存在的。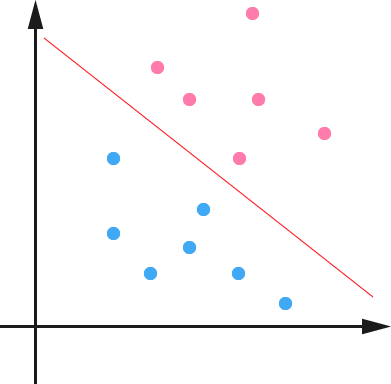

如图所示，两种颜色的点分别代表两个类别，红颜色的线表示一个可行的超平面。在进行分类的时候，我们将数据点 \(x\) 代入\(f(x)\)中，如果得到的结果小于 0，则赋予其类别-1 ，如果大于0则赋予类别1。如果\(f(x) = 0\)，则很难办了，分到哪一类都不是。事实上，对于\(f(x)\)的绝对值很小的情况，我们都很难处理，因为细微的变动（比如超平面稍微转一个小角度）就有可能导致结果类别的改变。理想情况下，我们希望\(f(x)\)的值都是很大的正数或者很小的负数，这样我们就能更加确信它是属于其中某一类别的。

从几何直观上来说，由于超平面是用于分隔两类数据的，越接近超平面的点越“难”分隔，因为如果超平面稍微转动一下，它们就有可能跑到另一边去。反之，如果是距离超平面很远的点，例如图中的右上角或者左下角的点，则很容易分辩出其类别。

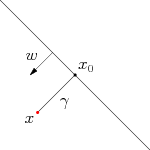
实际上这两个Criteria是互通的，我们定义 functional margin 为\(\hat{\gamma} = y(w^{T}x + b) = yf(x)\)，注意前面乘上类别\(y\)之后可以保证这个 margin 的非负性（因为\(f(x) < 0\) 对应于\(y = -1\)的那些点），而点到超平面的距离定义为 geometrical margin 。不妨来看看二者之间的关系。如图所示，对于一个点\(x\)，令其垂直投影到超平面上的对应的为\(x_{0}\)，由于\(w\)是垂直于超平面的一个向量（请自行验证），我们有

$$x = x_{0} + \gamma\frac{w}{\|w\|}$$

又由于\(x_{0}\)是超平面上的点，满足\(f(x_{0}) = 0\)，代入超平面的方程即可算出

$$\gamma = \frac{w^{T}x + b}{\|w\|} = \frac{f(x)}{\|w\|}$$

不过，这里的\(\gamma\)是带符号的，我们需要的只是它的绝对值，因此类似地，也乘上对应的类别\(y\)即可，因此实际上我们定义 geometrical margin 为：

$$\tilde{\gamma} = y\gamma = \frac{\hat{\gamma}}{\|w\|}$$

显然，functional margin 和 geometrical margin 相差一个\(\|w\|\)的缩放因子。按照我们前面的分析，对一个数据点进行分类，当它的 margin 越大的时候，分类的 confidence 越大。对于一个包含\(n\)个点的数据集，我们可以很自然地定义它的 margin 为所有这\(n\)个点的 margin 值中最小的那个。于是，为了使得分类的 confidence 高，我们希望所选择的 hyper plane 能够最大化这个 margin 值。

不过这里我们有两个 margin 可以选，不过 functional margin 明显是不太适合用来最大化的一个量，因为在 hyper plane 固定以后，我们可以等比例地缩放 \(w\)的长度和\(b\)的值，这样可以使得\(f(x) = w^{T}x + b\)的值任意大，亦即 functional margin\(\hat{\gamma}\)可以在 hyper plane 保持不变的情况下被取得任意大，而 geometrical margin 则没有这个问题，因为除上了\(\|w\|\)这个分母，所以缩放\(w\)和\(b\)的时候 \(\tilde{\gamma}\)的值是不会改变的，它只随着 hyper plane 的变动而变动，因此，这是更加合适的一个 margin 。这样一来，我们的 maximum margin classifier 的目标函数即定义为

$$\max \tilde{\gamma}$$

当然，还需要满足一些条件，根据 margin 的定义，我们有

$$y_{i}(w^{T}x_{i} + b) = \hat{\gamma}_{i} \geq \hat{\gamma}, \quad i=1,\dots,n$$

其中\(\hat{\gamma} = \tilde{\gamma}\|w\|\) ，根据我们刚才的讨论，即使在超平面固定的情况下，\(\hat{\gamma}\)的值也可以随着\(\|w\|\)的变化而变化。由于我们的目标就是要确定超平面，因此可以把这个无关的变量固定下来，固定的方式有两种：一是固定\(\|w\|\)，当我们找到最优的 \(\tilde{\gamma}\)时\(\hat{\gamma}\)也就可以随之而固定；二是反过来固定\(\hat{\gamma}\)，此时\(\|w\|\)也可以根据最优的 \(\tilde{\gamma}\)得到。处于方便推导和优化的目的，我们选择第二种，令\(\hat{\gamma} = 1\)，则我们的目标函数化为：

$$\max \frac{1}{\|w\|}, \quad s.t., y_{i}(w^{T}x_{i} + b)\geq 1, i=1,\dots,n$$

通过求解这个问题，我们就可以找到一个 margin 最大的 classifier ，如下图所示，中间的红色线条是 Optimal Hyper Plane ，另外两条线到红线的距离都是等于\(\tilde{\gamma}\)的：

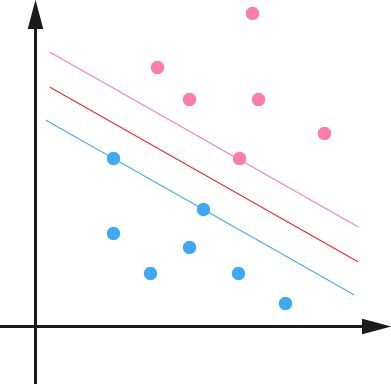
到此为止，算是完成了 Maximum Margin Classifier 的介绍，通过最大化 margin ，我们使得该分类器对数据进行分类时具有了最大的 confidence （实际上，根据我们说给的一个数据集的 margin 的定义，准确的说，应该是“对最不 confidence 的数据具有了最大的 confidence”——虽然有点拗口）。不过，到现在似乎还没有一点点 Support Vector Machine 的影子。很遗憾的是，这个要等到下一次再说了，不过可以先小小地剧透一下，如上图所示，我们可以看到 hyper plane 两边的那个 gap 分别对应的两条平行的线（在高维空间中也应该是两个 hyper plane）上有一些点，显然两个 hyper plane 上都会有点存在，否则我们就可以进一步扩大 gap ，也就是增大\(\tilde{\gamma}\)的值了。这些点呢，就叫做 support vector ，嗯，先说这么多了。

ps: 本文开头那张照片来源于这里。Allaboutinquiry 同学留言揭露典故真相啦： 😀

关于这个同学举牌子的典故我知道，我也是CMU的。这是在2009年在Pittsburgh举行的G20峰会现场外面。很多反对G20的，支持G20的都来凑热闹。我们这位同学也来了，鱼目混珠的高举Support Vector Machine的牌子。很多老美就晕了，你说你支持加强控制二氧化碳排放我懂，你支持的的这个Vector Machine是个什么东西啊？然后这个同学搞笑的目的就达到了。