飞帅云:“三十功名尘与土,八千里路云和月。莫等闲,白了少年头,空悲切。”可我在耶鲁两年多了,基本一事无成。既没有像当年那样死磕Lasso和Boosting,也没有能追随Deep Learning 的浪潮。曾经真的以为人生就这样了,平静的心拒绝再有浪潮。斩了千次的情丝却断不了,百转千折她将我围绕。有人问我她究竟是哪里好?我想我是鬼迷心窍。
1 向来痴
她就是LMM,我给她起了一个美丽的中文名:“林妹妹”。
对我这种工科男,与林妹妹相知相识,是需要一段奇缘。从在浙大本科自动化专业入学,到港科大的电子系博士快毕业,曾经有且仅有一次机会与她相识,还是被很傻很天真的我错过了。现在不管我怎么念“菠萝菠萝蜜”,时光还是不会倒流的。我只是想,如果上天可以给我一个机会再来一次的话,我会对她说八个字:“我们好像在哪见过?”然而,有缘人终归是有缘人,奇妙的感觉就在点火的那一刹那。
2010年,夏。
香港,清水湾。
海浪拍打着沙滩,伴随着风的欢笑,涌出蔚蓝的一片。
那一天,香港科大来了一位远方的客人,便是我现在耶鲁的老板。在他的演讲中,提到了一个故事。本人平生听了很多故事,但是我认为这个是最精彩的。据一些专家估算,人类身高的差异(统计学上用方差来描述),70%左右由遗传决定。另一批专家利用最新科技做了全基因组扫描,发现了大约100多个遗传变异点与人类身高显著的相关。这批专家就用这些显著的变异点去解释身高的方差时,惊讶地发现它们只能解释5%!从5%到70%,我靠,这中间的差距也太大了吧!“到底哪批专家是砖家,或者都是?”这个问题在我脑子里油然而生。然而以我的智慧,只猜中了开头,却猜不到结尾。林妹妹的出现让剧情峰回路转……
如今,专家们基本已达成共识:不要只是去关注那些显著的变异点!虽然这些不显著的变异点每一个的作用都比较小,但是他们总的作用却不能忽略!如果把那些不显著变异点的作用一起考虑进去,就能解释身高方差的45%,如果再考虑上那些没有被直接观察到的变异点的影响,就基本上接近70%。如何能把那么多不显著变异点的作用都优雅地考虑进去呢?这里就需要林妹妹了。
前面讲的故事是当今生命科学中最重要的课题之一。2009年的时候,科学家们还专门给这个故事起了一个名字–“missing heritability”,用今年流行的语言翻译过来就是“遗传物质都去哪儿了?”身高只是其中一个例子,对很多复杂疾病,比如糖尿病,高血压,精神分裂症等,科学家们也发现类似的情况。这个missing heritability 类似于物理学上的暗物质,感觉它存在却看不到它。林妹妹的出现让我们真实地测量到遗传学中的“暗物质”,并确认它的存在。
2 从此醉
好了,是时候停止卖萌,进入主题了。LMM全称是Linear Mixed Model(混合线性模型)。她血统高贵,与现代统计学之父Ronald Fisher提出的随机效应一脉相承。上个世纪50 年代,Charles Henderson 为她打造了国际一流的统计性质(BLUE and BLUP)1,他的学生Shayle Searle 更是为她配上了“黑客帝国(Matrix)” 的装备,从此她的名字将永远记入统计学的史册。1991年,statistical science上有一篇很经典的文章“That BLUP is a Good Thing: The Estimation of Random Effects”2,里面谈到了她许多超一流的品质。事实上,我们在实践中已经用到了她很多好的性质,只不过我们以前不知道罢了。
现在从她的一副黑客帝国装备说起,因为这副装备低调奢华有内涵:
$$ \begin{equation} \begin{aligned} \mathbf{y}&=\mathbf{X}\mathbf{\beta} + \mathbf{Zu}+\mathbf{e},\\ \mathbf{u}&\sim \mathcal{N}(\mathbf{0},\sigma^2_u\mathbf{I}),\\ \mathbf{e}&\sim\mathcal{N}(\mathbf{0},\sigma^2_e\mathbf{I})\\ \end{aligned} \end{equation} $$
这里$\mathbf{y}\in\mathbb{R}^n$是回归问题中的因变量,$\mathbf{X}\in\mathbb{R}^{n\times d}$和$\mathbf{Z}\in\mathbb{R}^{n\times p}$分别是固定效应和随机效应的设计矩阵,$\mathbf{e}\in\mathbb{R}^n$是随机误差,$\mathbf{\beta}\in\mathbb{R}^d$和$\mathbf{u}\in\mathbb{R}^p$分别是固定效应向量与随机效应向量,$n,d,p$分别是样本数目,固定效应的个数以及随机效应的个数。这里$\mathbf{y},\mathbf{X},\mathbf{Z}$是给定的,需要估计的是$\mathbf{\beta},\mathbf{u},\sigma^2_{u},\sigma^2_{e}$。 看到这里,我知道大部分童鞋已经有点晕了:啥叫固定效应,啥叫随机效应?先解释什么叫随机效应。 我相信大家都理解随机数,简单点说,他们就是从某一个分布里面随机抽出来的数,这些数不是固定的,但是他们总体上服从某种规律(即某种分布),比如服从正态分布。之所以用“随机效应”而不是用“随机数”,是为了描述设计矩阵的每一列所对应的变量对因变量$\mathbf{y}$的作用,比如在上述模型中的$\mathbf{u}$是一个$p$维的向量,它的每个元素即$u_j,j=1,\dots,p$都来自于正态分布$\mathcal{N}(0,\sigma^2_{u})$,$u_j$即是$\mathbf{Z}$的第$j$列对$\mathbf{y}$的效应。现在来解释啥叫固定效应,一句话,固定效应就是非随机效应。当固定效应与随机效应在一起的时候,就是所谓的mixed model。 注意千万不要把mixed model与mixture model 混为一谈!因为前者是被动在一起的,后者则是主动在一起的,想分都分不开。
既然是被动在一起,把二者拆开就比较容易。如果只看固定效应那一部分,
$$ \mathbf{y}=\mathbf{X}\mathbf{\beta} + \mathbf{e}, \quad \mathbf{e} \sim \mathcal{N}(\mathbf{0},\sigma^2_e\mathbf{I}), $$
这就是最基本的多元线性回归,$\mathbf{\beta}$的最优解由最小二乘法(Least square)给出,即$\hat{\mathbf{\beta}}_{LS}$,它的统计性质由高斯马尔科夫定理(Gauss–Markov Theorem)保证,比如$\hat{\mathbf{\beta}}_{LS}$是所有无偏估计中方差最小的。如果只看随机效应那一部分,
$$ \begin{aligned} \mathbf{y}&= \mathbf{Zu}+\mathbf{e},\\ \mathbf{u}&\sim \mathcal{N}(\mathbf{0},\sigma^2_u\mathbf{I}),\\ \mathbf{e}&\sim\mathcal{N}(\mathbf{0},\sigma^2_e\mathbf{I}), \end{aligned} $$
相信大家对上式也不会陌生。比如,看过Pattern recognition and machine learning (by Bishop, C.)的第三章Linear Models for Regression的童鞋应该会发现:当$\lambda=\frac{\sigma^2_{e}}{\sigma^2{_u}}$时,求解上式与下式得到的解则是完全等价。
$$ \min_{\mathbf{u}}\|\mathbf{y}-\mathbf{Z}\mathbf{u}\|^2+\lambda\|\mathbf{u}\|^2, $$
不同的是,这里的$\lambda$通常由交叉验证确定,而估计前面式子中的参数($\sigma^2_{u}$与$\sigma^2_{e}$)则另有办法。在机器学习中,大家把它叫做Evidence approximation,统计学里面把它叫经验贝叶斯(Empirical Bayes)。
现在可以再把二者合在一起了,但这里涉及到一个重要的问题。举一个简单的例子,有$n$个数据点$(x_1,x_2,\dots,x_n)$,每个数据点$x_i\in \mathbb{R}$都独立地来自$\mathcal{N}(\mu,\sigma^2)$。对$\sigma^2$的最大似然估计是$\tilde{\sigma}^2=\sum_i(x_i-\bar{x})^2/n$,这里$\bar{x}=\sum_i x_i/n$是均值。但是,正如大家所知道的,对$\sigma^2$的无偏估计应该是$\hat{\sigma}^2=\sum_i(x_i-\bar{x})^2/(n-1)$,因为在估计均值的时候已经消耗掉一个数据了。为了补偿在有若干个固定效应情况下对方差估计的偏差,有一个办法应运而生,它的名字叫REML (REstricted Maximum Likelihood,约束极大似然或限制极大似然)。
前面提到的探索遗传学中的暗物质是对LMM一次高端大气上档次的运用。遗传的变异会引起身高的差异,那么身高有多大程度上是由遗传因素决定的?翻译成统计学语言:用遗传变异点数据究竟能解释身高方差的百分之多少?回过头来再看,$\mathbf{y}$中是$n$个样本($\sim 5000$) 的身高数据,$\mathbf{X}$的每一列对应一个协变量,比如年龄、性别,基因组变异点的数据都放到$\mathbf{Z}$中,其中每一列对应一个变异点的数据。为了写出$\mathbf{y}$的边际分布,需要对$\mathbf{u}$和$\mathbf{e}$积分,
$$ \mathbf{y}\sim\mathcal{N}(\mathbf{X}\mathbf{\beta},\mathbf{ZZ}^T \sigma^2_{u} + \sigma^2_{e} \mathbf{I}). $$
注意$\mathbf{X}\mathbf{\beta}$并不影响$\mathbf{y}$的方差。Heritability定义为:
$$ h^2=\frac{p{\sigma}^2_{u}}{p{\sigma}^2_{u}+{\sigma}^2_{e}}, $$
这里$p\sigma^2_{u}$是遗传因素解释的方差($p$是变异点个数,大约是50万到100万这个范围),$\sigma^2_{e}$是非遗传因素造成的方差。启动REML 以后,就能得到($\hat{\sigma}^2_{u},\hat{\sigma}^2_{e}$),然后算出heritability。
3 水榭听香,指点群豪戏
“脚步不能达到的地方,眼光可以到达。”抬望眼,满城尽是LMM,如下图所示。由于篇幅所限,我只能简单地介绍一部分。
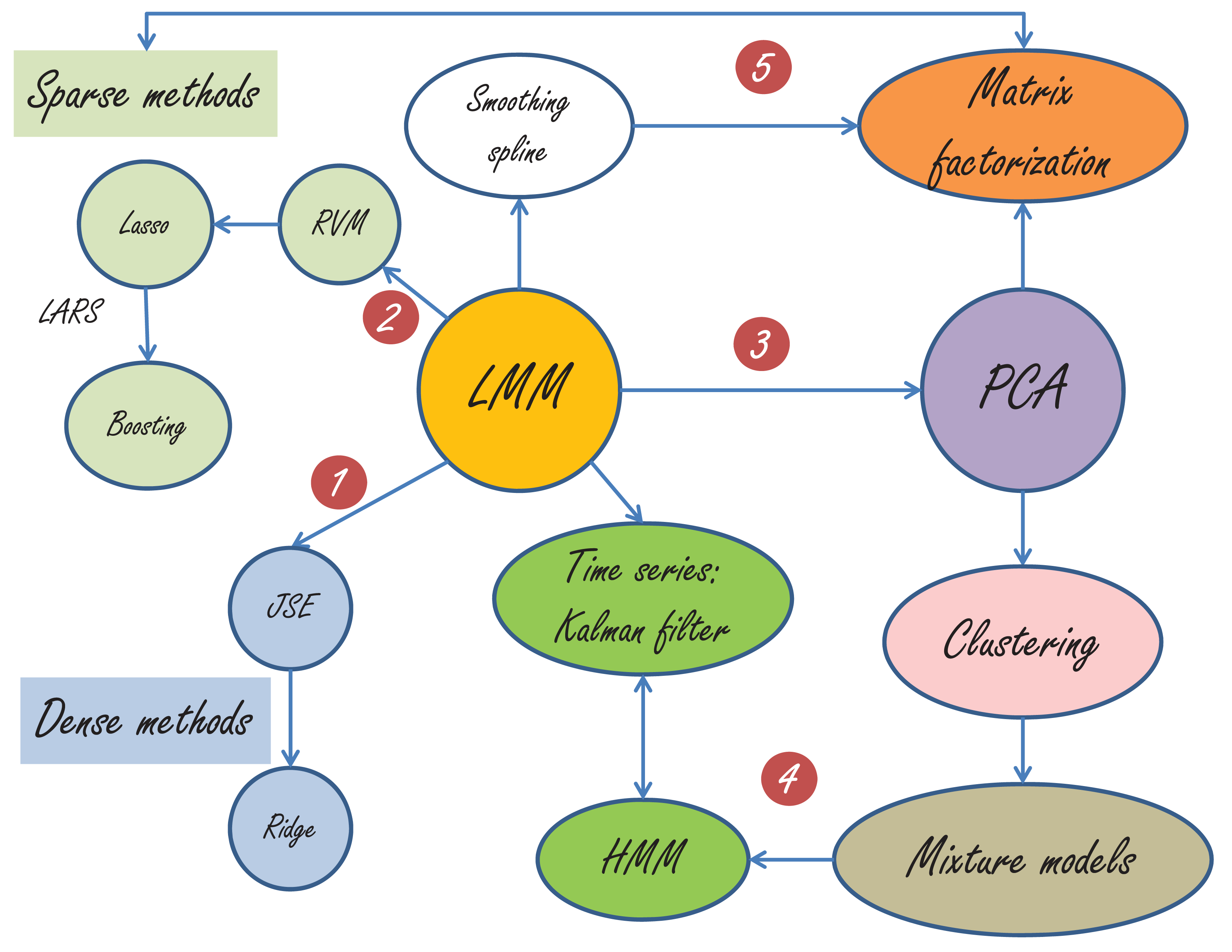
LMM与很多经典方法的关系图
第一,LMM与JSE-Ridge Regression的关系最为明显。当没有固定效应,$\mathbf{Z}$变为单位矩阵的时候,LMM就变为了JSE(这个时候需要$\sigma^2_{e}$ 是已知的,不然会有可辨识性的问题。在JSE(James-Stein Estimator)的问题中,$\sigma^2_{e}=1$,更详细的描述请参考我的《那些年我们一起追的EB》)。LMM与Ridge 的关系,前面已经讲过了。
第二,RVM(relevance vector machine)如下:
$$ \begin{aligned} \mathbf{y}&= \sum_j \mathbf{Z}_j u_j+\mathbf{e},\\ u_j&\sim \mathcal{N}(0,\sigma^2_{u_j}),\\ \mathbf{e}&\sim\mathcal{N}(\mathbf{0},\sigma^2_e\mathbf{I}), \end{aligned} $$
RVM与LMM的差别是:RVM允许每个随机效应$u_j$有自己的方差$\sigma^2_{u_j}$,而LMM中所有的随机效应(random effects)具有同样的$\sigma^2_{u}$。 从RVM 到Lasso(Least Absolute Shrinkage and Selection Operator),只需要假设$\{\sigma^2_{u_j}\}$来自指数分布,详情参见Bayesian Lasso。Lasso,LARS和Boosting已经成为统计学与计算科学史上的一段佳话,最好的文献当然是Efron教授的Least Angle Regression,喜欢看故事的童鞋可以看我的《统计学习那些事》。
第三,LMM与PCA(Principal Component Analysis)的联系似乎不是那么直接,因为这里已经从监督学习走向了非监督学习。然而,当PCA被赋予概率的解释后,天堑变通途。这篇里程碑式的文章就是Probabilistic principal component analysis by Tipping and Bishop。PCA与clustering的亲密关系暴露在本世纪初,clustering和mixture models的关系嘛,应该是不言而喻的。
第四,大家都知道,Mixture models里面是有一个隐状态,比如在做clustering的时候,这个隐状态就用来表明数据点与cluster的隶属关系。当这些隐状态不再是独立等分布的时候,比如,后一个状态取决于前一个状态的时候,HMM便应运而生。HMM与卡曼滤波(Kalman filter)基本上可以看做孪生兄弟,一个为离散状态而生,一个为连续状态而来。LMM与卡曼滤波的关系在“BLUP is a good thing”这篇雄文中早有讨论。当年学控制的我与卡曼滤波有过初步接触,但是却与LMM 失之交臂,还好在耶鲁与LMM再续前缘。
第五,如今的Matrix factorization已经是令人眼花缭乱了,因为这里加入了很多sparse(包括low-rank)与smoothing的技术。但不可否认,PCA依然是矩阵分解中最重要的一种,奇异值分解依然是这里最重要的数学基石。
面对如此波澜壮阔的模型表演,不知道大家会如何感想?这里我先引用Terry Speed在“BLUP is a good thing”的评论里的最后一段话
In closing these few remarks, I cannot resist paraphrasing I.J. Good’s memorable aphorism: ‘To a Bayesian, all things are Bayesian.’ How does ‘To a non-Bayesian, all things are BLUPs’ sound as a summary of this fine paper?
大师的话值得久久回味……我自己总结的话,来点通俗易懂的,还是这句“天下武功,若说邪的,那是各有各的邪法,若说正的,则都有一种‘天下武功出少林’的感觉”。
4 杏子林中,商略平生義
“眼光不能到达的地方,精神可以飞到。”
“随机还是非随机?”是一个问题,甚至是一个哲学问题。或许,我们参一生也参不透这道难题。爱因斯坦说:“上帝不玩骰子。”然而,麦克斯韦却说:“这个世界真正的逻辑就是概率的计算。” 电影《美丽心灵》的纳什也在追问“到底什么才是真正的逻辑”。最后他在获得诺奖时说:“ 我一直以来都坚信数字,不管是方程还是逻辑都引导我们去思考。但是在如此追求了一生后,我问自己:‘逻辑到底是什么?谁决定原由?’我的探索让我从形而下到形而上,最后到了妄想症,就这样来回走了一趟。在事业上我有了重大突破,在生命中我也找到了最重要的人:只有在这种神秘的爱情方程中,才能找到逻辑或原由来。”这是我听到的最美的答案。
如果回到工程实践的话,或许我们应该追问:“为什么引入随机效应后会有如此神奇的疗效?”Efron教授在他的一篇文章中称赞James-Stein Estimator:“This is the single most striking result of post-World War II statistical theory”。 我想,我们应该可以从JSE 中寻找到一些蛛丝马迹。JSE的原问题是:现已观察到$N$个$z$值,即$[z_1,z_2,\dots,z_N]$,还知道$z_i$独立地来自以$\mu_i$为均值,1为方差的正态分布,即$z_i|\mu_i \sim \mathcal{N}(\mu_i,1)$, $i=1,2,\dots,N$.问题是:如何从观察到的$\mathbf{z}=[z_1,z_2,\dots,z_N]$估计$\boldsymbol{\mu}=[\mu_1,\mu_2,\dots,\mu_N]$?最大似然法和James-Stein Estimator给出解答分别是(更多细节参考《那些年,我们一起追的EB》):
$$ \hat{\mathbf{\mu}}_{ML} = \mathbf{z},\quad\hat{\mathbf{\mu}}_{JS} = \left( 1- \frac{N-2}{||\mathbf{z}||^2}\right)\mathbf{z}. $$
对JSE的理解有很多不同的角度,个人觉得从下面的这个角度看过去是非常精彩的。如果我们把$\mu_i,i=1,\dots,N$看做是随机,那么我们可以认为他们来自某一个分布$\mathcal{G}(\mu)$,随着$N$的增大,我们对$\mathcal{G}(\mu)$的估计就会越准确。原来看似独立的$z_i$却能通过这样一个分层结构(见下图)来共享信息。虽然$N$很小的时候,$\mathcal{G}(\mu)$是没法估计准确的,但幸运的是,这里的$N$并不要求太大。可以证明,只要$N\geq3$,JSE就比MLE好。这就是Efron教授所说的“learning from others”。如果用更加数学的语言来刻画信息共享,其实就是Bias-Variance trade-off。当信息共享的时候,偏差增加了少许但方差却大大降低。
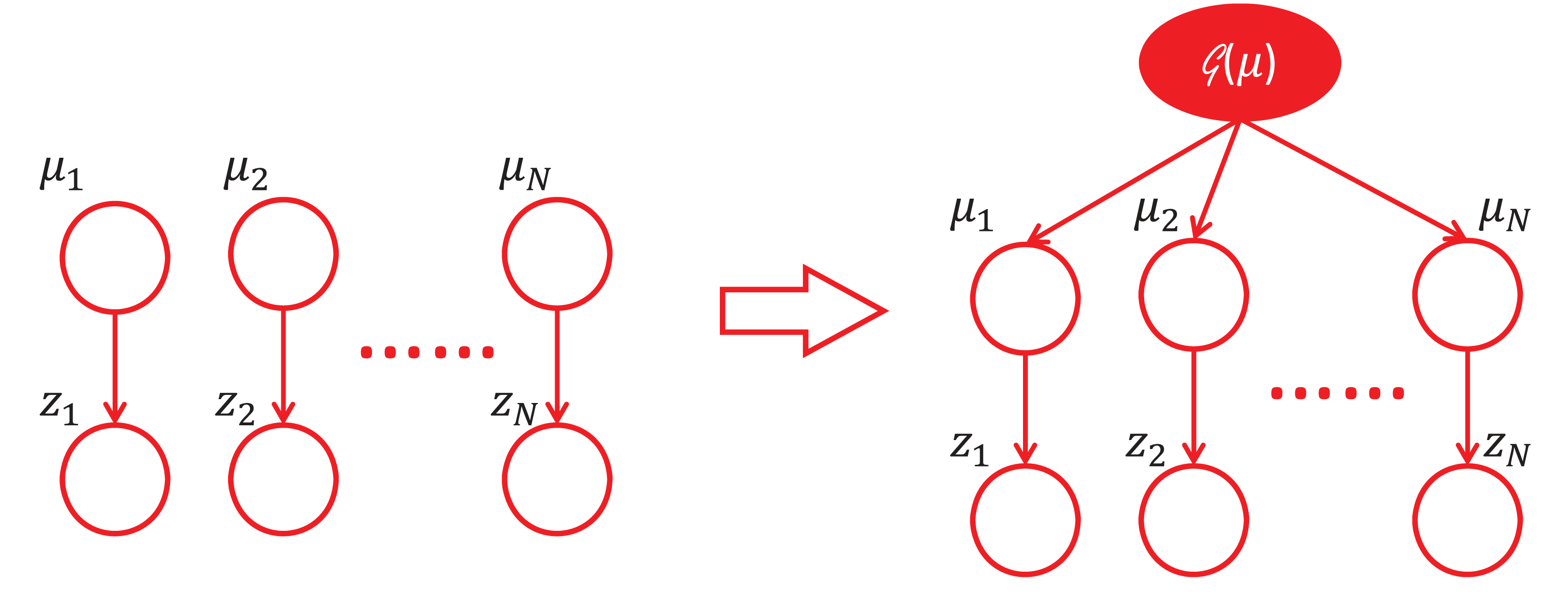
5 须倾英雄泪
James Watson在他的《双螺旋》一书的序言中写道:“科学的发现很少会像门外汉所想像的那样,按照直截了当、合乎逻辑的方式进行。事实上,科学的进步(有时是倒退)往往是人为事件。在这些事件中,人性以及文化传统都起着巨大的作用。”
“庾信平生最萧瑟,暮年诗赋动江关。”这是张益唐教授为“孪生素数猜想”作出巨大贡献后接受采访时引用的诗句。听罢,令人感慨万千。
昔时因。
今日意。
“胡汉恩仇”,须倾英雄泪。
最后附上本文的pdf原稿供下载:LMM_Yale
-
BLUE 和 BLUP 分别表示 Best Linear Unbiased Estimate (最佳线性无偏估计)和 Best Linear Unbiased Prediction (最佳线性无偏预测) ↩︎


发表/查看评论