NBA总决赛刚结束不久,今年最幸福的肯定就是勇士球迷了。宇宙勇的球迷一定很关心一个东西,因为它决定着你看到的是海啸组合还是铁花兄弟——它就是手感。
但是,手感真的会忽冷忽热吗?
你肯定会说这问题怎么这么蠢,打过球的谁没有篮筐大的像海洋的时候?别急。。让我先介绍下这问题的背景。
缘起
n年以前,斯金纳在一系列经典的鸽子实验中展示了如何通过强化学习让鸽子学会各种习惯(现在很火的深度学习中的强化学习的名字是从心理学中借用来的,二者有关联但也很不一样),比如下面的视频展示了斯金纳是怎么在一分钟内把鸽子调教到会原地转圈的。
但斯金纳的手段远不止于此,通过改变不同的强化方式,他发现了一个有趣的现象。假如你在鸽子做出某个动作后让食物掉出来,那鸽子很快就会学会这个动作,就像上面学会原地转圈那样;如果鸽子不管做什么你都不放食物出来,那鸽子很快就啥都不做了。这些都很合理,但当你放出食物的时机与鸽子的动作毫无关系时(比如固定每隔20秒掉食物),那鸽子会展现出各种奇怪的强化行为——有的会不断地逆时针转圈、有的会向左边扭一下头再去看有没有吃的、有的会使劲地晃动脑袋……这些行为也很好解释,当鸽子做出某个动作时食物碰巧掉出来了,鸽子就会认为它一定做对了什么,从而重复这个动作,而过一会食物果然又掉出来了……最终鸽子就这样学会了各种奇奇怪怪的动作,斯金纳把这称之为“鸽子的迷信”1。
你说鸽子笨嘛,脑袋那么小,难怪容易迷信。那请你想想赌场里赌徒们千奇百怪的禁忌、想想星座、想想本命年的红内裤……我们这个物种的许多成员又好到哪里去呢?事实上我们和鸽子一样,非常擅长从随机中看出“规律”(Apophenia)——如果不是更擅长的话2-5。iTunes早期的随机播放是完全随机的,结果收到用户投诉,说咋这么不随机?乔布斯不得不采用了更复杂、完全不随机的算法,才让用户满意。用乔布斯自己的话说:“We’ve actually added Smart Shuffle to make it less random. But it seems more random.”
这种根深蒂固的本能自然有着进化上的道理,在一个没规律的地方看出规律你可能也就多晃几下脑袋,但假如食物真的是因为晃脑袋掉出来的你却没发现,那你就得饿死了。既然错过规律比找错规律代价要大得多,那我们肯定宁愿多找出些“规律”。这种认知偏见自然没有逃过心理学家的眼睛,于是有一天几个心理学家琢磨着:“人们认为的手热会不会也是纯粹的随机现象呢?”
手热迷思
1985年Gilovich、Vallone和Tversky对此进行了研究,结果很惊人,他们发现手热效应是不存在的6。这篇论文与心理学界对人类非理性行为的认知完全相符,所以被迅速接受并成为经典。因为在圈内广为人知,它常常直接被称作GVT论文——和爱因斯坦的EPR论文一样,以三位作者名字的首字母命名。之后不少人重复了这个研究,大部分都得出了类似的结论——手热只是幻觉。这话题果壳网其实介绍过,但并不让人满意,因为文章最后一笔带过的Joshua Miller的最新研究恰恰是整个话题峰回路转的最高潮,所以我重新写一下。
GVT论文里进行了这么几项研究:
- 调查球迷的态度,大部分人认为手热是存在的(当然);
- 分析了1980-81赛季76人队的比赛数据,分析方法是这样的:统计出刚刚连续命中一个(或数个)篮和刚刚连续投失一个(或数个)篮情况下的命中率,对比后发现刚刚投中过球并没有让你变得更准,事实上命中率反而更低了;
- 把每个76人球员的赛季投篮数据分成四个四个的一段,统计热得发烫(四中三或全中)、普通(四中二)和冰凉(四中一或全失)的出现频率,假如手感确实会忽冷忽热,那它们的分布与用平均投篮命中率算出来的随机分布应该有区别,但并没有;
- 采访了76人队队员,绝大多数都相信手热现象,并认为自己有过手热的经历(当然);
- 以上的分析有个显而易见的问题,就是干扰项太多:手热的时候对方可能会对你防守更严,你可能会因为自信而浪投……所以GVT又分析了罚球数据,第一罚命中会让你第二罚更准吗?他们分析了1980-82两个赛季凯尔特人的罚球数据,没有发现显著性;
- 然后又找来了康奈尔大学一些校队院队球员进行受控实验,让他们在无对抗情况下各投篮100次,然后进行了和2、3中一样的分析,依然无果;
- 最后他们研究了对手热的感知。在校队队员每次投篮前,他们让投篮者和队友预测球会不会进,结果自我预测和投篮命中的相关性只有0.02,队友预测和命中的相关性是0.04。
不难看出整个研究做的挺细致,质量上乘,结论也是理聪最爱的那种,所以很快就流传开来。古尔德写过,卡尼曼也写过,科学家们乐此不疲地教育着头脑简单的运动员和大众:“都是幻觉,都是幻觉!”然后几十年过去了……
“手热迷思”迷思
第一个转折来自于对GVT论文效力的研究:假如我用电脑模拟手热效应存在的投篮数据,然后用GVT的方法去分析,你猜怎么着?大多数情况下是检测不出手热的7。也就是说不管手热存不存在,他们的方法都检测不出来——统计效力(power)不足。这一下就推翻了GVT的大部分论证。不过这只说明了他们的方法不对,结论也许碰巧还是对的呢?
2015年Joshua Miller为GVT送上了最后一击,他们发现GVT(和许多后续研究)都犯下了一个极其微妙的数学错误,在纠正后,这些数据不仅没有否定手热现象,反而强烈地支持它8。除了重新分析数据,他们还指出了GVT在受控实验部分设计上的一些不足,并进行了改进的实验,发现了显著的效应9。
那这个微妙的错误是什么呢?我们先来做几道数学题。
你拿一个硬币,扔啊扔,然后连扔出了三个正面,请问你下一次扔还是正面的概率是多少?
你说这太简单了,独立事件嘛,赌徒谬误嘛,哪怕我连扔出一百次正面下一次得到正面的概率都还是0.5。
嗯没错,那现在你再拿一个硬币,扔一百次,每当连扔出三个正面时你就把下一次投掷的结果记下来,最后你的结果里正反面各占多少?
这个问题的答案——惊人地——不是0.5。为了证明它真的不是0.5,我们看一下最简单的情况,总共扔三次,然后统计连续两次正面出现的概率。
| 序列 | HX的次数 | HH的次数 | HH的概率 |
|---|---|---|---|
| HHH | 2 | 2 | 1 |
| HHT | 2 | 1 | 0.5 |
| HTH | 1 | 0 | 0 |
| HTT | 1 | 0 | 0 |
| THH | 1 | 1 | 1 |
| THT | 1 | 0 | 0 |
| TTH | 0 | 0 | - |
| TTT | 0 | 0 | - |
| HH的预期概率 | 5/12 |
你看,预期概率确实不是0.5,而且可以证明它一定小于0.5,也就是说用这种方法计算的话,连续多次正面后确实有更大的概率出现反面。我相信这简单的数数你肯定看懂了,但你的直觉未必能跟上,所以我再多说几句,看看能不能帮你从直觉上也理解它。
首先,直觉是没错的,扔出多少次正面都不会影响后续的结果,这体现在第三列的和一定是第二列和的一半,但第四列的和却一定小于第二列的一半。区别在哪呢?在于$E(X)/E(Y) \neq E(X/Y) $。$E(HH)/E(HX)$一定等于0.5,但$E(HH/HX) $就不一定了。这样我们就理解了为什么这个概率不是0.5,那它为什么还一定会小于0.5呢?我们假想这样一张表,它的前两列与上表完全一样,但第三列的数都正好是第二列的一半,从而第四列就都是0.5。假想表与上表的第三列虽然不一样,但和是一样的,所以我们可以在不同行间挪动第三列的数值,这行加一点,那行就减掉一点,始终保持第三列的和不变,这样最终我们可以得到上表。这种操作会给第四列的均值带来什么影响呢?会让它变小。理由是这样的:记第二列第$i$行的数为$n_i$,第三列第$i$行的数为$k_i$,那第四列的相应数值就是$k_i / n_i $,当我们从第$i$行挪一单位第三列的值给第$j$行时,第四列的和的变化是$1/n_j -1/n_i $。所以假如$n$大的那些行$k$倾向于大于$n/2$,那第四列的均值就会小于假想表的均值——0.5。观察上表你会发现这个倾向是存在的,所以均值确实小于0.5。那这个倾向是怎么来的呢?来源于重复计算。也就是HHT会被我们当做HH和HT算两遍,这在序列长度为4的情况下会看的更清楚,如果我们把HHHT算作HH、HH、HT,那H多的序列HH会异常的多,算出来的概率就会小于0.5,如果我们不重复计算,只把它拆成HH、HT,那就不会有任何偏差,预期概率=0.5,这点你可以自行验证。
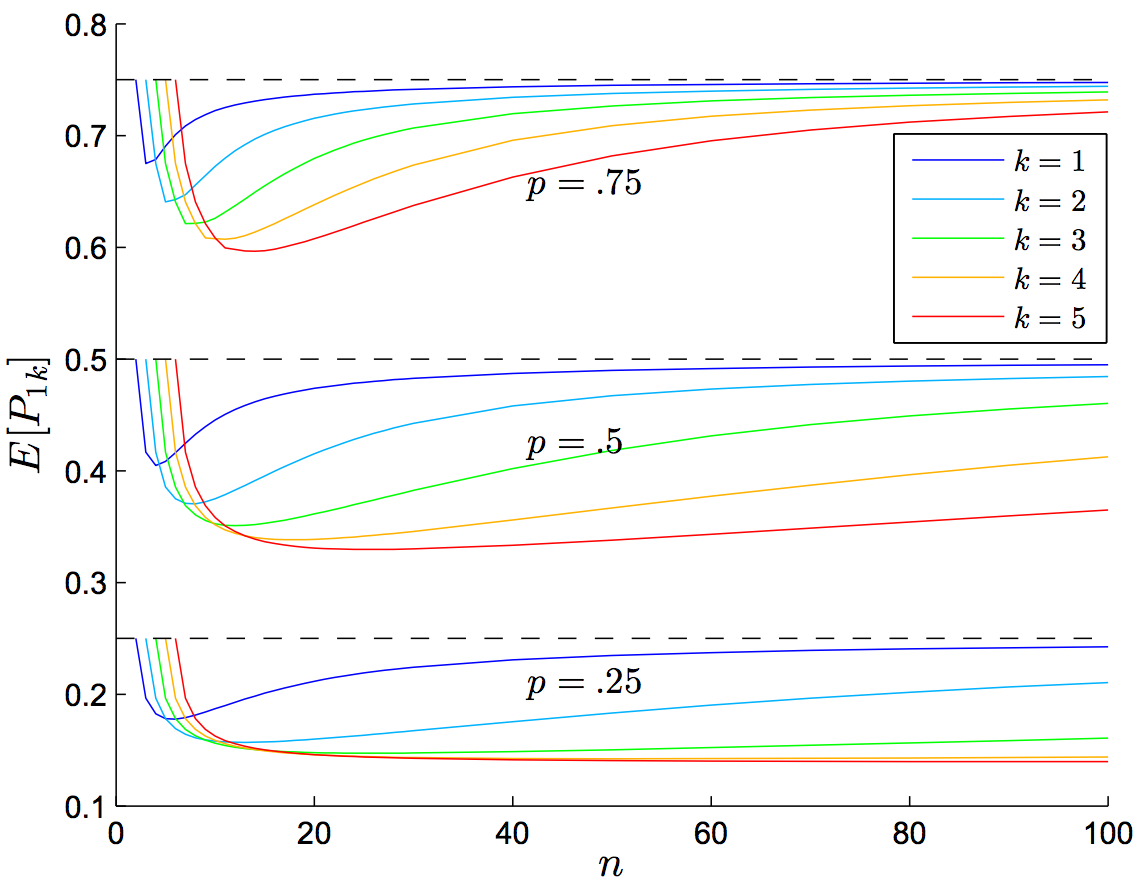 下一次投掷是正面的概率对不同的投掷次数n、连续出现正面的次数k和单次投掷出现正面的概率p作图。“扔一百次,观察连扔出三个正面后下一次的结果”对应着n=100,k=3,p=0.5,所以下一次是正面的概率约为0.46。图片取自论文8。
下一次投掷是正面的概率对不同的投掷次数n、连续出现正面的次数k和单次投掷出现正面的概率p作图。“扔一百次,观察连扔出三个正面后下一次的结果”对应着n=100,k=3,p=0.5,所以下一次是正面的概率约为0.46。图片取自论文8。
假如你还没想明白,这篇论文10提供了这个问题由易到难的各种变形,其中还包括一道Google以前的面试题:
有个国家特别地重男轻女,每家都一直生一直生直到生出儿子为止(只要生出儿子他们就不再生了),请问这个国家人口中女性的比例预期是多少?
我这里就不再展开了,希望你已经能理解答案并不是官方给的0.5。
好了,说了那么多脑筋急转弯,这些跟手热不热有什么关系呢?请你再看一遍GVT里的第6项研究:他们让球员各投100次,然后算出连续命中三次(或两次、一次)之后下一次的命中率。他们的做法和从一个给定次数的样本中统计连续三次正面后下一次硬币结果的做法是一模一样的,所以这个估计是有偏的。而且偏差很大,在他们的数据里达到了8%。他们拿着这个有偏的估计发现手热效应不存在,这恰恰证明了手热是存在的,当你把8%加回去,原来不显著的现在全都显著了。而8%是什么概念呢?库里这赛季的三分和总命中率分别是41.1%和58%,扣掉8%在后卫里对应的大概是德文哈里斯和德隆威廉姆斯。所以手热效应不仅存在,而且还很重要。
至此GVT中还比较有意义的研究就剩第7个:人们感受不到谁手正热,哪怕自己都感受不到。假如真感受不到那哪怕手热了意义也不太大,但人们真的感受不到吗?再看一遍他们的结论,他们发现的是人们的预测和实际投篮结果的相关性只有零点零几,这难道还不说明感受不到?这种论证忽视了一个问题,那就是即使你能准确的感受到队友手热,也不可能准确预测投篮结果,因为哪怕队友的手热得发烫,命中率从平时的45%变成了55%,那也还是有将近一半的概率投丢。我们不妨做个计算,假设队友平时的命中率是45%,手热时命中率是55%,手热出现的几率是15%,你能完美地知道队友处于手热状态,所以在他手热时你全预测投进,手不热的时候全预测投丢,这样相关性会是多少?
以X表示投篮,Y表示预测,1表示进,0表示没进,显然X、Y都服从伯努利分布。 $$\mu_X = p_X = 0.85*0.45 + 0.15*0.55 = 0.465 $$ $$\mu_Y = p_Y = 0.15$$ $$\sigma_X = \sqrt{p_X(1-p_X)}$$ $$\sigma_Y = \sqrt{p_Y(1-p_Y)}$$ $$cov(X, Y) = E[(X-\mu_X)(Y-\mu_Y)] = E[XY] - \mu_X \mu_Y = 0.55*0.15 - 0.465*0.15 = 0.01275$$ $$corr(X, Y) = \frac{cov(X, Y)}{\sigma_X \sigma_Y} = 0.072$$ 所以即使你能完美预测,预测和投篮的相关性也就是零点零几,因此GVT的原始数据并不能说明人们无法感受到手热。相关性这么低的原因在于二项分布是个很难准确估计的分布,命中率变化10%在观测上要很久才能看出来。Miller改进并重做了投篮预测实验,发现人们是能够准确感受到手热状态的。
科学危机
GVT只不过是这几年科学可重复性危机的冰山一角,在心理学领域大量重复失败的研究里11,GVT的论文质量算是比较好的了。我再随便举两个出了问题的研究:
- 哈佛美女教授Amy Cuddy在TED上的著名演讲,认为强势的身体动作(power pose)可以助你成功。这个演讲在TED上观看次数超过四千两百万,是历史第二多,当时在社交网站上也掀起了一波"Fake it until you make it"的鸡汤潮。结果不仅没重复出来,原论文的另一个作者还直接在网上写了一封公开信,声称观点已变,现在认为power pose效应不存在了,建议其他研究者别再浪费时间。
- 社会启动效应(social priming)。这个领域发端于John Bargh1996年的研究12,他们让学生从五个词里挑四个出来造句,一组学生拿到的是普通词,另一组拿到的是与老年相关的词汇,比如健忘、秃顶、满脸皱纹、佛罗里达,实验完后他们告诉学生穿过大厅去另一个地方做下一组实验,但他们关心的其实既不是造句也不是下一个实验,而是学生穿过走廊的速度,他们发现那些被老年相关词汇启动(prime)了的学生比另一组慢了将近一秒。这个惊人的结果启发了大量后续研究,十几年来整个领域欣欣向荣,Bargh的原论文已被引用了四千多次。人们发现啥都能拿来prime,比如考卷字迹模糊能让你考得更好,让你描述一个严厉教授的样子也能让你在常识测验中表现更好……卡尼曼在《思考:快与慢》里举了整整一章各种惊人的例子,最后得出结论,
然而,问题的关键是要接受相关研究的结果,而不是对此心存怀疑。这些结果不是捏造出来的,也不是统计上的偶然现象。你别无选择,只能接受这些研究的主要结论是正确的这一事实。
“你别无选择”、“你必须承认”……好吧,现在Bargh的最初实验和其他许多实验都没能重复出来,整个领域风雨飘摇。Bargh前几年没憋住还发了通火,又引来更多非议。这里有一篇手把手教你做social priming研究的文章,辛辣搞笑,推荐阅读。当然我不是说这领域一定就全错了,毕竟我也不是专业人士,我只是觉得怎么看我应该都还是有点选择的。
所以心理学到底是怎么落到这步田地的呢?
统计困局
There are three kinds of lies: lies, damned lies, and statistics. - Benjamin Disraeli
The Earth Is Round (p < .05) 13
一方面其实是因为心理学比许多同样危机重重的学科更开放、关注度更高,另一方面它也确实有着自身的问题。心理学中广泛使用的p值——以及更一般的,整个假设检验范式,在这次危机中起着核心作用。越来越多人知道单纯地依赖这套范式不好,但大多数人还没意识到它到底有多糟,对此,备受尊敬的前美国心理学会会长保罗·米尔(Paul Meehl)是这么说的14,
I believe that the almost universal reliance on merely refuting the null hypothesis as the standard method for corroborating substantive theories in the soft areas is a terrible mistake, is basically unsound, poor scientific strategy, and one of the worst things that ever happened in the history of psychology.
人们对p值有着太多的误解15,连美国统计学会都少见的出来说了几句16,如何改进也是众说纷纭19-22,这里是几点主要的。
Confusion of the inverse
这个问题已经是老生常谈了。p值的含义是在零假设成立的情况下观察到手上数据(或比手上数据更极端的数据)落在拒绝域的概率,也就是说它指向的是数据,但大部分情况下我们根本不关心这,我们关心的是凭着手上的数据,假设有多大的可能成立。我们关心的是假设,不是数据。xkcd的这幅漫画很好地体现了这种区别。
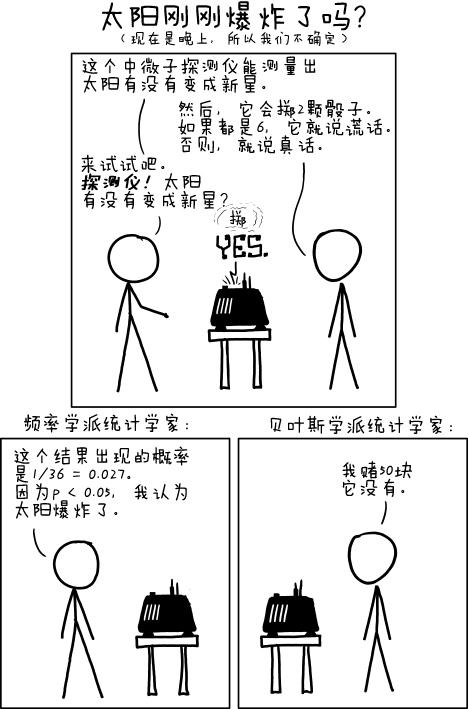
这里我们根本不关心骰子出现这种结果的概率有多大,我们关心的是太阳爆炸的概率有多大。虽然这二者是成正比的,但比例系数(先验概率)可大可小(这里太阳爆炸的先验概率就很小),所以从前者常常推不出太多关于后者的信息,而我们又极度地渴望后者,结果就是p值总是被误用和误读,当它难得被正确使用时,它却是在回答错误的问题。
The garden of forking paths23
假设检验的另一个严重问题是多重比较,说到这肯定有人想到了xkcd的另一幅经典漫画。

这当然是幅很好的漫画,但也有些误导性。它容易让人以为只有这样明显地p-hacking才算多重比较,而大部分科学家肯定是不会这样做的,所以他们就不觉得自己会有多重比较的问题。不是这样的,哪怕你自始至终只检验了一个假设,也依然可能会涉及多重比较,让我们来看个例子。
进化心理学之父/母图比(John Tooby)、柯斯米德斯(Leda Cosmides)夫妇提出了一个设想:人类的进化史充满了战斗,而上肢力量对战斗显然很重要,上肢强壮的人更有可能积极参与掠夺和守护资源,即对资源有更强的占有欲,现代社会不打架了,但这种部落时代的心理依然保留了下来,可能会以其他形式体现出来,比如他们可能会更反对政府的再分配政策。然后他们就去收集数据,测量了几百个人的二头肌,并询问他们对再分配政策的态度,果然发现胳膊越粗的人越反对再分配,p=0.007。
多好的研究,有什么问题吗?没有任何问题——除了结果是我编的。他们并没有发现手臂越粗的人越反对再分配,他们发现的是男性手臂越粗就越反对,但女性身上没有这种效应。
很合理啊,战斗、掠夺、守卫资源本来就是男性的事,完美符合进化史,有什么问题吗?没有任何问题——除了结果是我编的。他们也没有发现男性手臂越粗越反对再分配,他们发现的是社会地位高的男性手臂越粗越反对,社会地位低的手臂越粗反而越支持24。
也很合理啊,地位低当然喜欢再分配嘛,有什么问题吗……
有啊,假如他们发现胳膊越粗的人越反对再分配他们会发表文章并视为对自己理论的支持吗?我相信会的;假如他们发现男性手臂越粗越反对再分配他们会发表文章并视为对自己理论的支持吗?我相信会的;假如他们这些都没有发现,但是发现年纪大的男性手臂越粗越反对再分配但年纪轻的男性反之他们会发表文章并视为对自己理论的支持吗?我相信会的,因为年长的人往往积累了更多财富需要捍卫嘛;假如他们发现年纪轻的男性手臂越粗越反对再分配但年长的男性反之他们会发表文章并视为对自己理论的支持吗?我相信会的,因为年轻正是自我打拼赚资源的时候,再分配不符合这种雄心壮志……
我随口编的这些“解释”也许并不都合理,我也不认为Tooby夫妇会有任何学术不端(做为进化心理学的忠实拥趸,我很尊敬他们),我想说的正是即使你十分正直诚实,你完全在数据的指引下寻找结论,你自始至终只做了一次假设检验,你依然可能涉及多重比较——潜在的多重比较25,而这也正是假设检验的危险之处。当然这种情况还叫多重比较已经不合适了,更好的叫法是多重建模(multiple modeling)26,或者研究者自由度(researcher degrees of freedom)。这种自由度可以在参与者浑然不觉的情况下轻易地让p值产生巨大的变化27,因此也非常地难以避免。一个简单的解决办法就是把研究显式地分为探索阶段和验证阶段,探索阶段有了任何新发现,就固定数据分析方法,进行预注册实验,看看在验证阶段是否能重复出来。这适用于成本低廉的实验,但有些实验重复起来太不现实,那就只好采用其它方法,贝叶斯多层模型是一个不错的选择,因为partial pooling,它能在很大程度上自动校正多重比较问题28。
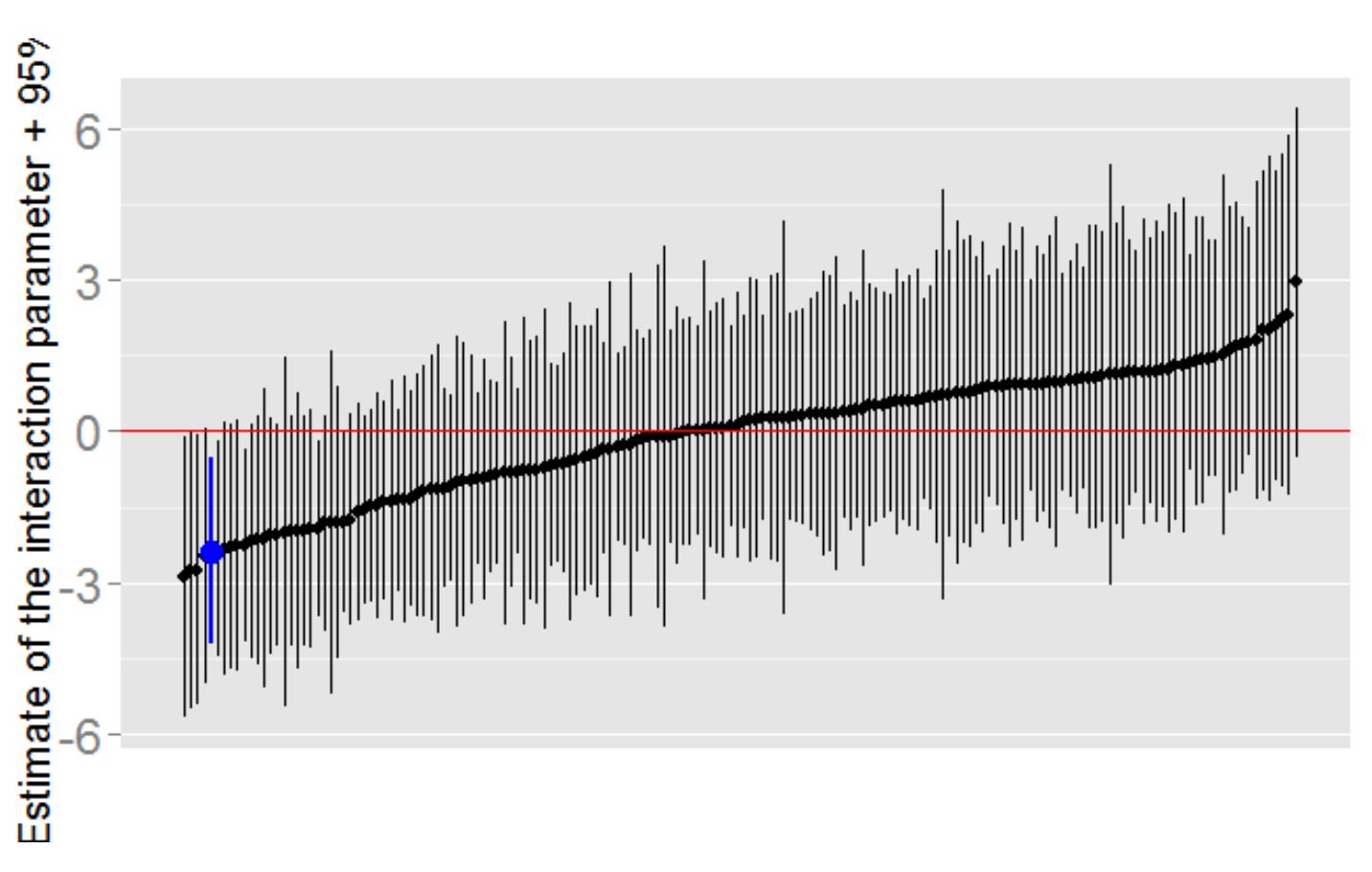 一项研究发现单身女性在排卵期内会更有可能投票给奥巴马,相反,处于排卵期的非单身女性更愿意投给罗姆尼,变化值超过十个百分点29,这背后当然也有一套进化理论啦,但让我们来看下数据处理上可能的自由度吧:大姨妈后的第几天到第几天算排卵期?那些大姨妈不规律的样本要不要排除掉?如果调查对象对上次大姨妈的时间不够确定,要排除掉吗?多不确定才排除?怎么样算非单身?处于暧昧期的算吗?一垒呢?二垒呢?三垒呢?四垒呢?五垒呢?……Andrew Gelman认为整个数据至少有168种完全合理的处理方式,然后他把168个置信区间全算了一遍,得到上图,蓝线对应的是论文29实际采用的分析方法。
一项研究发现单身女性在排卵期内会更有可能投票给奥巴马,相反,处于排卵期的非单身女性更愿意投给罗姆尼,变化值超过十个百分点29,这背后当然也有一套进化理论啦,但让我们来看下数据处理上可能的自由度吧:大姨妈后的第几天到第几天算排卵期?那些大姨妈不规律的样本要不要排除掉?如果调查对象对上次大姨妈的时间不够确定,要排除掉吗?多不确定才排除?怎么样算非单身?处于暧昧期的算吗?一垒呢?二垒呢?三垒呢?四垒呢?五垒呢?……Andrew Gelman认为整个数据至少有168种完全合理的处理方式,然后他把168个置信区间全算了一遍,得到上图,蓝线对应的是论文29实际采用的分析方法。
The law of small numbers
在GVT的讨论里我们已经提到了效力不足的问题,教科书上对效力的说法是效力不足你就不能发现该发现的东西,现实比这糟的多,你不是没有发现该发现的,而是会发现一堆乱七八糟不该发现的东西。
首先,在效力不足的情况下,得到的p值会很不稳定(p dancing19),不显著还好,要是碰巧显著了,恭喜你,你又为学术共同体贡献了一个虚假发现。
(* Mathematica codes *)
<< HypothesisTesting`
nSamples1 = 11; (* Power ≈ 0.5 *)
nSamples2 = 25; (* Power ≈ 0.8 *)
nTrials = 10000;
σ = 2;
effect = 1;
p1 = p2 = {};
Do[
result1 = RandomVariate[NormalDistribution[effect, σ], nSamples1];
AppendTo[p1, LocationTest[result1, μ_0 = 0]];
result2 = RandomVariate[NormalDistribution[effect, σ], nSamples2];
AppendTo[p2, LocationTest[result2, μ_0 = 0]];
, {nTrials}]
Histogram[{p1, p2}, {0.05}, "Probability",
AxesLabel -> {"p value", "Frequency"},
ChartLegends -> {"Power ≈ 0.5", "Power ≈ 0.8"},
ChartStyle -> "Pastel", LabelStyle -> Medium, ImageSize -> 500]
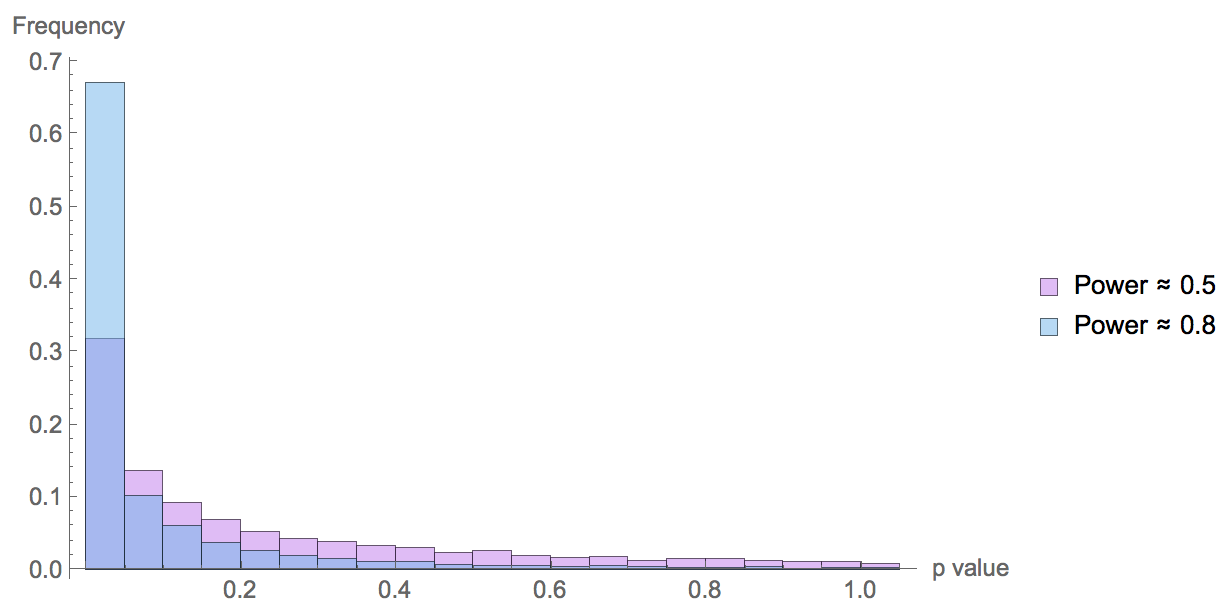 效应值=1,样本标准差=2,对应的Cohen’s d=0.5,在心理学中被认为是中等效应。图上是模拟实验一万次得到的p值分布,最左边的柱对应着显著(p≤0.05),不难看出p值的不稳定。
效应值=1,样本标准差=2,对应的Cohen’s d=0.5,在心理学中被认为是中等效应。图上是模拟实验一万次得到的p值分布,最左边的柱对应着显著(p≤0.05),不难看出p值的不稳定。
其次,如果你在效力不足时得到了显著性,你很有可能会严重高估效应值,甚至连符号都可能是错的,这被称作抖S(ign)和M(agnitude)型错误30。S怎么也能算错误
(* Mathematica codes *)
pe1 = pe2 = {}; (* Point estimate *)
Do[
result1 = RandomVariate[NormalDistribution[effect, σ], nSamples1];
If[LocationTest[result1, μ_0 = 0] ≤ 0.05, AppendTo[pe1, Mean[result1]]];
result2 = RandomVariate[NormalDistribution[effect, σ], nSamples2];
If[LocationTest[result2, μ_0 = 0] ≤ 0.05, AppendTo[pe2, Mean[result1]]];
, {nTrials}]
Histogram[{pe1, pe2}, Automatic, "Probability",
AxesLabel -> {"Point estimate", "Frequency"},
ChartLegends -> {"Power ≈ 0.5", "Power ≈ 0.8"},
ChartStyle -> "Pastel", LabelStyle -> Medium, ImageSize -> 500]
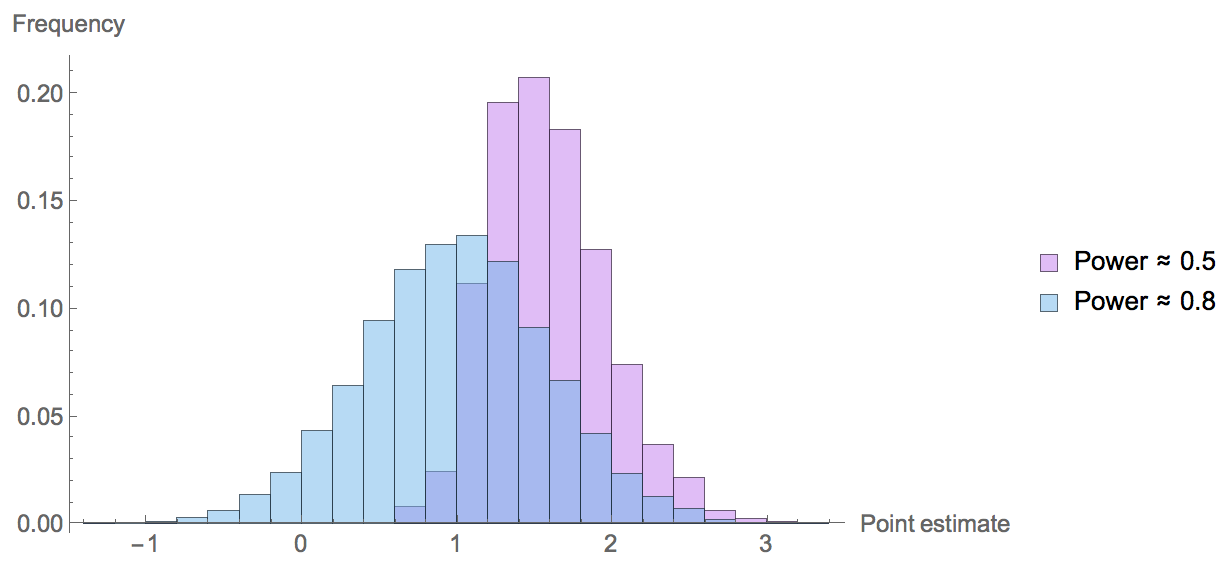 真实效应值=1,可以看出即使效力=0.8估计值也普遍偏高。
真实效应值=1,可以看出即使效力=0.8估计值也普遍偏高。
那现实中科学研究的效力如何呢?这几年有人评估了神经科学领域的研究,认为中位效力只有21%31;经济学领域则不超过18%32;Cohen在62年评估了心理学界,认为如果研究的是小效应,当时的效力大概只有18%,中等效应的话有48%33;二十几年后人们用Cohen的方法又研究了一遍,发现心理学研究效力不仅没有改善,还恶化了34。这些研究有的有争议35,但即使最乐观的研究者大概也不会认为现在的平均效力超过0.5。其实早在1971年,后来的诺奖得主卡尼曼和他的好基友特沃斯基就注意到他们的同行常常严重高估实验的效力,仿照大数定律,他们把这种认为小样本也能很好地代表整体的倾向命名为小数定律36。这种错误倾向有多难以克服呢?你只要再读一遍论文作者的名字就知道了。看到了吗?特沃斯基,他就是GVT里的那个T啊,连他都掉到自己发现的坑里去了。而卡尼曼也没好到哪去,几个月前刚刚有人指出《思考:快与慢》中关于social priming的那一章是效力严重不足的……卡尼曼爽快地承认了错误。
为了避免让你产生这届心理学家不行的误解,我们来做个测试。
Satoshi Kanazawa是伦敦政经的进化心理学家,他热衷于扩展Trivers–Willard假说,所以论文题目看起来常常是这样的,

他还合著过一本书,书名也很简单粗暴,叫*Why Beautiful People Have More Daughters*(中译本叫《生猛的进化心理学》)。我对政治不正确的研究没有任何意见——如果不是喜闻乐见的话,但是你的方法得靠谱啊。Kanazawa的研究充满了各种统计错误30,37-39,我们以上图最后一篇论文为例,他分析了Add Health数据集,这是最大、最综合的关于青少年的长期追踪数据集,从人们还是青少年时开始追踪,四次回访,记录了这些人的许多信息,其中两个与这里的话题有关,一是这些人的孩子的性别,二是调查人员会对被采访者的外貌打分,从最丑到最美共有五档。Kanazawa选取了第三次回访中有孩子的人(2972个)进行了分析,他发现最美的一档生女孩的可能性比其他人高8个百分点(56% vs 48%),p < 0.05,所以,beautiful parents have more daughters。首先这里存在明显的多重比较问题,第一档和其他档比显著了,和最丑的一档、倒数第二档比怎么反而都不显著了呢?为什么不把最美的两档和剩下的三档比,假如这么比显著的话Kanazawa会不提吗?……这里更好的办法显然是对外貌和出生性别建模,弄个回归方程啥的,而不是进行假设检验。不过即使那样也是毫无意义的,为什么呢?因为,你觉得2972个样本在这里效力够吗?
假如放平时我相信大部分人都觉得够了,快三千个样本,在心理学里是很大型的研究了,今天你还可以看到很多研究就几十个样本呢。但现在我这么一问你应该也知道答案是不够,那我再问,你觉得多少样本才够呢?
我们还是来算算吧。生男生女是个伯努利事件,假设我们现在有数量相等的两档人,每一群人数是n,从过往的研究中我们知道人类在极度营养不良下生女孩的概率大约会增加3%39,所以长相对性别比的影响极不可能是8%,撑死2%吧。一群人出生性别比的样本标准差是$\sqrt{p(1-p)/n} \approx 0.5/\sqrt{n} $,两个群体的差值的标准差就是$0.5 * \sqrt{2/n} $。2%的效应想要显著,意味着2%得大于两倍标准差, $$0.02 > 2 * 0.5 * \sqrt{2/n} \Rightarrow n > 5000 $$ 这是一个群体的数量,两个群体就至少得要一万人。这已经是很乐观的估计了,假如效应值是1%(实际情况很可能更小),那样本数就得要四万了。需要这么大的样本的原因和分析投篮数据时是一样的——二项分布难以估计准确。所以这项研究的问题与假设检验无关,改用贝叶斯也救不回来,这个研究想法出生的那刻就已经被宣判死刑了。
现在你知道通过直觉判断效力有多容易出错了吗?这也是效力计算为何如此重要的原因。对于那些复杂的实验,可能没办法从数学上进行计算,那可以先在已知数据上进行验证,例如用电脑生成的手热数据去验证GVT的统计方法。我这里还有两个特别有趣的例子,一个是关于功能性磁共振成像(fMRI)的。你应该读过一些科学家一边让被试做某类事情一边用fMRI扫被试大脑,然后得出XX脑区负责XX行为的研究。09年的时候有人想这玩意到底可不可靠啊,于是他们就用fMRI去扫描了一条三文鱼的大脑,结果发现了信号,好像没什么不对?可是,他们扫的是一条死三文鱼啊40(这项研究众望所归地拿到了搞笑诺贝尔奖)。同年还有另外两篇论文指出当时fMRI实践中大量存在的几个统计问题41,42,自那以后大部分研究者都提高了警惕,整个领域发展的更健康了(至少比心理学好)。而就在今年,有人把神经科学中常用的一些研究方法应用到红白机处理器上去,想看看这些方法到底能不能帮助我们理解一个信息处理系统,结果不能算特别乐观43。这篇文章太新了,结论可以再讨论,不过这个研究想法是非常好的。
和物理学的比较
在说了那么多假设检验的坏话后,有两个问题是无法回避的:其他学科,包括物理学,也有使用假设检验,为什么没这么多问题?假设检验在它的提出者手里为什么表现的挺好,不然后来也不会被这么广泛地使用?这是两个好问题,通过对比成功范例可以让我们更好地理解心理学里的假设检验到底哪出了问题,以及为什么这种问题更多的是因为使用上、而不是理论上的错误44,45。
粒子物理学里也使用假设检验,虽然他们往往不说p值,而说几个标准差,但是一个意思,那为什么希格斯粒子的发现就显得那么可靠?首先,他们使用的p值很小。发现新粒子的黄金标准是5个标准差,对应的p值大概是三百万分之一。这还是开新闻发布会时候的数字,等写成论文发表的时候ATLAS的数据已经达到5.9个标准差,对应的p值是$1.7*10^{-9}$46。
其次,物理学的原假设是很强的,希格斯粒子不存在是个完全有可能的假设,需要很强的数据才能否定它,所以当它真的被否定时,对互补假设是强大的支持。心理学则完全不是这样。心理学里最常见的零假设是X和Y没有关系(相关=0),或者稍微强一点的也就是X对Y的效应是正的(或者负的),否定这样一个假设你得到的结论也不过是X和Y有关系,至于多大的关系、重要吗,则完全无法回答。而考虑到心理学中各因素的普遍联系,X和Y没有关系几乎是一个必然错误的假设,所以推翻它毫无意义。经期跟投票倾向有关吗?当然有关啊,而且不仅经期有关,你的身高体重鞋码三围无名指长度姓名首字母织毛衣的技巧……都会有关好吗?只不过有些相关太小了需要极大的样本才能检测出来,Paul Meehl曾经分析过一个有45个变量、包含57000个明尼苏达高中生资料的数据集,计算了所有变量的两两关系,结果其中92%是显著的,71%的p值小于$10^{-6}$47,所以有人说假设检验本质上是对于样本数的检验,就是这个意思。这种弱检验导致了心理学和物理学的一个重要区别:随着测量手段的进步,物理学里否定一个假设越来越难了,从而得到的结论也越来越可靠;而心理学里否定零假设却越来越容易了,你放眼望去哪都是效应,整个学科却没什么进展。这个方法论上的区别最早还是由Meehl注意到的,所以也被称作Meehl’s paradox14,48,49。
最后,物理学从理论假设到实验数据的链条紧实,实验数据可以很有效地作用在理论上。什么意思呢?当一个理论对现实做出预测时,它往往需要涉及一些辅助假设,举例来说,从长得好看的人多生女孩有进化优势(理论假设)推出在Add Health数据集中最美的一档会比其他人多生女孩(观测)时,我们暗中引入了许多辅助假设,比如好看的女性往往也嫁给社会地位高的男性,假如好看女性的基因会让她多生女孩,那成功男性的基因会不会导致多生男孩呢?Add Health的数据有代表性吗?对外貌的评分准确吗?Kanazawa使用的是第三次回访的数据,这数据有什么系统性偏差吗?……只有当这许多假设都成立的时候我们才能从理论推出预期的观测结果,反过来说,如果我们没观察到预期结果,也不意味着理论一定错了,因为也可能是辅助假设错了(这点后文还会进一步讨论)。所以如果整个逻辑链条过于松垮,实验对理论的验证效果就很弱。物理学中的推理当然也需要辅助假设,例如从希格斯粒子的存在到监视器上的信号,中间你至少需要一套关于加速器正确运作的假设。但物理学中的辅助假设常常可以被单独验证,比如LHC开机后,做的第一件事不是寻找希格斯粒子,而是先跑一组已知结果的实验,看看能不能重复出来(对LHC发现希格斯粒子的整个过程,《粒子狂热》是一部不错的纪录片)。这也顺便回答了本节开头的第二个问题:为什么假设检验在它的提出者手里应用的不错?首先,不管是费雪、内曼还是皮尔逊,他们要是看到今天心理学家对假设检验的使用都绝对会气得晕过去17,他们在提出这套方法时都特意强调了它的局限和问题;其次,费雪当时研究的是农业产量问题,理论(施肥会带来产量增长)到观测(那块施了肥的地玉米确实长得比较多)几乎零距离,只要效力足够,假设检验用起来是没什么问题的50。
抽屉效应/发表偏见
理论上,抽屉效应指的是因为期刊喜欢发表新发现,所以一个没得到显著性的研究会被锁在抽屉里,没有机会发表,从而你在期刊上看到的都是正面结果。抽屉效应确实是发表偏见的结果,但我不同意很多人因此把二者混为一谈,进一步的区分是有意义的。现实中,心理学的发表偏见不仅仅是不发表没有得到显著性的论文,如果只是这样,那倒也还好,毕竟有着研究者自由度,躺在抽屉里的文章其实不会太多。糟糕的是它们还不喜欢发表重复实验。心理学家极少重复前人的实验51,直接重复就更少了,他们偏好间接重复(conceptual replication),也就是把原始实验改来改去,理论上相符就好。这一恶习甚至连费曼都注意到了,在《别闹了,费曼先生》里他说,
其他许多错误比较接近于低品质科学的特性。我在康奈尔大学教书时,经常跟心理系的人讨论。一个学生告诉我她计划做的实验:其 他人已发现,在某些条件下,比方说是 X,老鼠会做某些事情 A。她 很好奇的是,如果她把条件转变成 Y,它们还会不会做 A。于是她计 划在 Y 的情况下,看看它们还会不会做 A。我告诉她说,她必须首先 在实验室里重复别人做过的实验,看看在 X 的条件下会不会也得到结 果 A,然后再把条件转变成 Y,看看 A 会不会改变。然后她才能知道 其中的差异是否如她所想像的那样。
她很喜欢这个新构想,跑去跟教授说;但教授的回答是:“不,你 不能那样做,因为那个实验已经有人做过,你在浪费时间。”这大约是 1947 年的事,其后那好像变成心理学的一般通则了:大家都不重复别 人的实验,而单纯地改变实验条件看结果。
错误链式反应
当我们把上面的种种因素拼在一起时,一个危机蔓延的动力学模型就呼之欲出了:
- 一个统计学不过关的研究者一天有了个新奇的想法,于是设计了一个实验(效力不足);
- 然后轻易地得到了显著性(研究者自由度);
- 他得到的效应值非常惊人,迅速吸引了大量眼球(M型错误);
- 其他研究者跟进,不直接重复,而是略微修改原来的实验(发表偏见);
- 大部分研究者也得到了显著性(还是研究者自由度);
- 许多结果也很惊人(还是M型错误);
- 少数不支持原假设的实验从没有得到发表,研究者甚至都没有把它们投出去,所以大多数人都不知道还有负面结果(抽屉效应);
- 重复4-7;
- 整个领域欣欣向荣,一切看起来那么的真实美好;
- 一天有人说:“要不我们来重复一下最初的实验吧……”
这似乎就是发生在social priming领域的事(最早的那篇Bargh的论文样本数是30……),不然你很难解释卡尼曼怎么会那么信誓旦旦。这个领域中不乏正直的人,仅仅用发表压力下的学术不端解释不了这样大规模的错误,只能说大家是真的相信。
这个模型并不是我的首创,again,Meehl1967年就提出了类似的看法48。这真的让人觉得很奇怪,Meehl在心理学界备受尊重,所有人都知道他,他60年代写的一系列批评假设检验的文章也很多人读,但就是没人听,几十年过去了整个学科还是老样子。到了90年代,Meehl自己都受不了了,又写了好几篇文章,其中有一篇无奈地说道52:
Ten years later, I wrote at greater length along similar lines (Meehl, 1978); but, despite my having received more than 1,000 reprint requests for that article in the first year after its appearance, I cannot discern that it had more impact on research habits in soft psychology than did Morrison and Henkel. Our graduate students typically plan and write their doctoral dissertations in blissful ignorance that “the significance test controversy” even exists, or could have a bearing on their research problems. This article (see also Meehl, 1990c) is my final attempt to call attention to a methodological problem of our field that I insist is not minor but of grave import.
然后现在危机降临,我们又把他翻了出来,希望这次心理学家能走点心吧……
应对
While it is easy to lie with statistics, it is even easier to lie without them. - Frederick Mosteller
正确的应对
现在来说下作为外人怎么消化这次危机吧。因为心理学的软科学性质,心理学家中最优秀的那一撮对方法论其实思考颇多(比如Meehl),所以他们对危机的到来早有准备,在《进化心理学》里,作者大卫·巴斯早早地为大家打好了预防针。他详尽地论述了进化心理学中不同的分析层次,从最一般的进化理论、到中级水平的进化理论、到具体的进化假设,每一级别既要兼容上一级,又要引入新的情境,从而得出更具体的预测。理论上确实存在某些现象能够证伪一般的进化理论(比如霍尔丹那句著名的“前寒武纪的兔子”),但现实中这些例子从来没有出现过,科学家们的日常工作还是集中于检验具体的进化假设。因为每个层次都引入了上一层次不具有的假设,所以证伪低层次的预测并不会自动推翻高层次的理论,对进化阐述的评估也因此不必依赖于某一个预测是否成功,而应该要看证据的积累量,这样就在核心理论与相对脆弱的外围间建立了有效的缓冲。
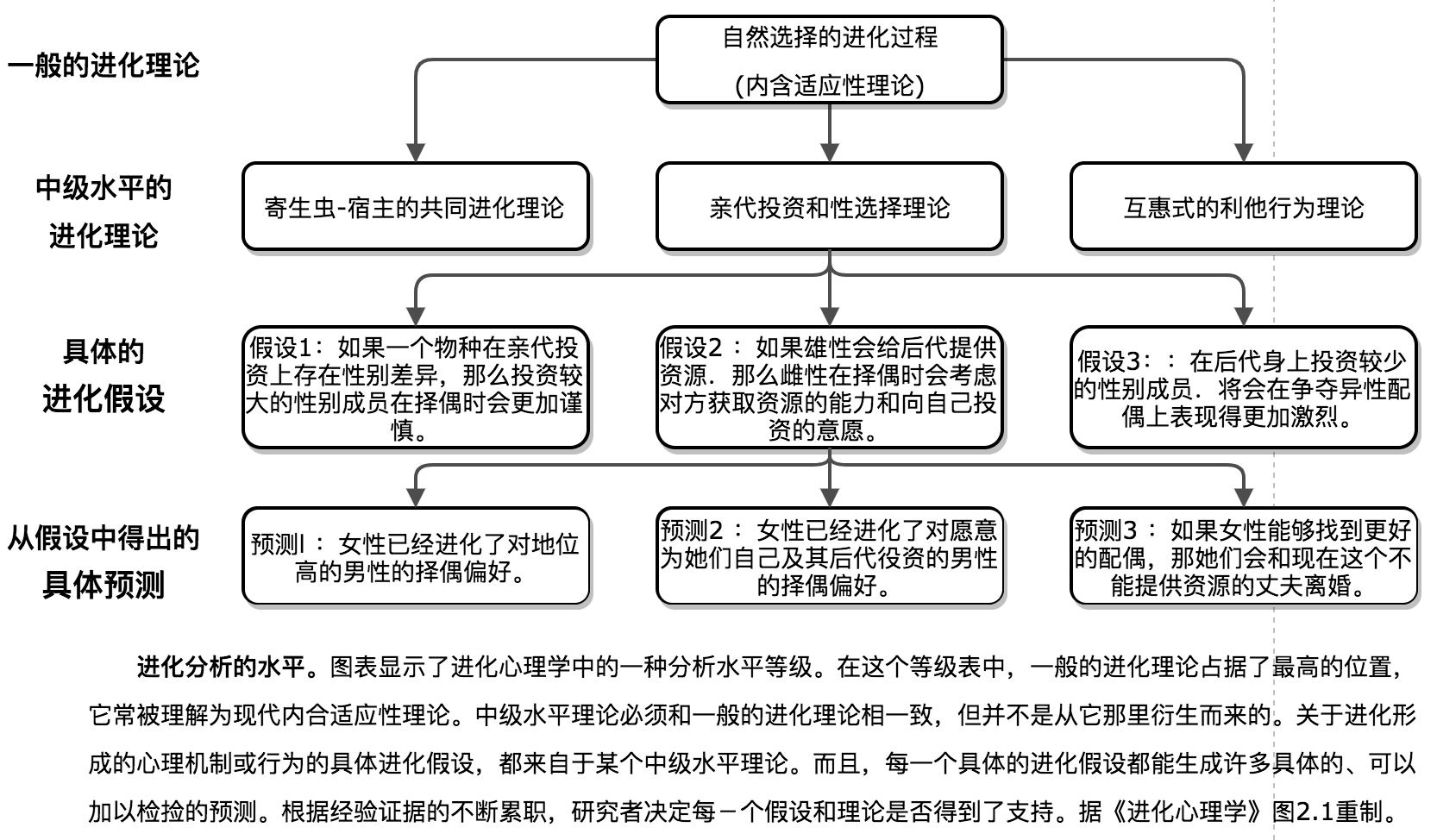 巴斯把整个第二章都贡献给了方法论,这在外国教材中很常见,而在中国人写的书里你基本看不到。就如辉格指出过的,中国人最需要普及的不是科学知识,而是科学哲学。
巴斯把整个第二章都贡献给了方法论,这在外国教材中很常见,而在中国人写的书里你基本看不到。就如辉格指出过的,中国人最需要普及的不是科学知识,而是科学哲学。
熟悉科学哲学的朋友一眼就能看出这套“硬核-保护带-具体假设”的模型正是拉卡托斯的理论,不过可能为了减轻学生负担,巴斯并没有在正文提到拉卡托斯,而是把他藏到了参考文献里(书里最后引用了一篇论文,题目叫Are evolutionary explanations unfalsifiable? Evolutionary psychology and the Lakatosian philosophy of science)。
通过拉卡托斯的框架可以很好地消化这次危机。经过这次危机,我的认知结构里关于心理学的许多具体假设完全改变了,一部分中级理论节点进行了适当更新,至于硬核……谁会怀疑进化论呢?但显然不是每个人都像我这样。
错误的应对
最常见的反应是虚无主义,当面对一个巨大的冲击时,全部否定也确实是最省事的办法,例如这是三联周刊科学记者土摩托。
再下一步就是相对主义。“科学并不总是对的”,每隔一段时间就会有那么一个人(一般是妹子)跟我说这句话,试图让我明白她相信的那套星座、中医……和科学应该有着同样的地位。如果你喜欢观察小粉红的话,你对这种“XX其实也会XX,所以XX和XX本质上是一样的”的论点一定不会陌生,不过小粉红太脏了,我还是举个高贵的女权主义的例子吧。Eve Ensler——前几年很火的《阴道独白》的作者,认为对女性的压迫在世界各地都是完全一样的(exactly the same),无论是在西方国家,还是在巴基斯坦、沙特阿拉伯和伊朗。
 正在被石刑处决的阿富汗少女。至于女性割礼的图,我就不放了吧。
正在被石刑处决的阿富汗少女。至于女性割礼的图,我就不放了吧。
最后就是解构主义了,不过像《跨越界线:通往量子引力的转换诠释学》这种东西实在不是我写得来的,还是把它留给各位后现代大神(经)吧。
你应该已经看出一个层次化的认知模型有多重要,否则稍不注意就不知道滑到哪里去了。但这自然带来了一个疑问,我们之前刚刚批评过心理学中从理论到观测的链条太过松垮,拉卡托斯的这个模型难道不也是这样吗?我的回答是这样的:辅助假设是不可避免的,你应该让它尽量的紧实(就像物理学中那样),但如果你拉得太过头,赋予了它多于事实能支撑的强度,那整个结构又会牵一发而动全身,也是不行的。至于怎么样的强度算恰当,这就取决于你的学术品味了。品味这东西一两句也说不清,我只能尽力而为,一方面我可以给你推荐一些比较好的书,品味都是多吃好东西培养出来的;另一方面我可以提供一些拇指法则,尽量帮你避开一些坑:
- 假如你对一项研究没把握,请假设它是错的53,54;
- 或者至少假设它的结论是严重高估的30;
- 如果一篇论文没有任何描述性统计的图,而全是假设检验的表,这是一个危险信号;如果只报告p值,完全没提效应值和置信区间,这是一个危险信号;如果使用了一堆假设检验却完全没有效力分析,这是一个危险信号;如果一篇文章有两个危险信号,你最好还是把它扔到垃圾桶去;
- 除非你特别特别感兴趣,社会启动效应和具身认知的东西先不要看了;
- 如果你对魔鬼经济学或格拉德威尔深信不疑,那你对心理学的信任太高了55;
- ……
结语
当代科学是在未知领域中的航行,走过的每一步都留下怯懦的教训,很多旅客宁可留在家里。——卡尔·萨根
写了这么多,可能有人会觉得”认识这世界好难啊“,但我想说的其实是它也好有趣啊。我知道大多数人可能无法体会这种乐趣,想想你有两个差不多的选择和只有一个选择时的心理状态,前者常常反而让你更焦虑。在不确定性中权衡、评估、决策是件费脑的事,我们渴望确定性。
对此进化给出的解法是观测-评估-权衡-决策-保持-迭代,举例来说,当一个人搬了新家,为了解决吃饭问题,他一开始会先多尝试几家餐馆,在评估比较后选出一些适合的(适合自己吃的、适合和朋友夜宵的、适合约妹子的……),之后这个决策过程就极大地自动化了,直到餐馆质量发生了足够大的变化,那就再启动新一轮的评估。当然各个环节并不是泾渭分明的,整个过程更类似于多臂老虎机(multi-armed bandit)问题的epsilon-decreasing解法,一开始探索性质多一些,然后慢慢减少。这样的做法牺牲了一定的准确性,但节省了大量的认知资源,是合理的。问题出在有些人的迭代频率如此之低,低到一辈子就评估那么一次。
 有的人25岁就死了,只是到75岁才埋葬。——富兰克林
有的人25岁就死了,只是到75岁才埋葬。——富兰克林
在生理上,这对应着大脑神经会在青春期经历一次大规模的修剪,之后就相对稳定下来。这种模式在停滞的传统社会是适应的,通过青春期躁动在部落/村庄中找到尽可能好的生态位,之后就安稳过日子吧,就算你想学也没啥东西能让你学了,但在现在这个时代,这种做法显然已经不合适了。可惜,很多人的大脑还没能跟上这个变化。
这些年我看着不少朋友变得日渐愚蠢偏执,曾经的理性和趣味在他们身上慢慢褪去,说实话有时候是很伤感的。当然我能够体谅,但依然觉得遗憾,所以写下这篇文章,希望你们能再出门看看。
参考文献
就我所见,对此次危机的统计方面讨论得最透彻的是Andrew Gelman,他的博客和文章是个不错的起点。假如你对更一般的方法论和科学哲学感兴趣,那Paul Meehl是绕不过去的。
1.Skinner, B. F. “Superstition” in the pigeon. Journal of Experimental Psychology: General 121, 273 (1992).
2.Herbranson, W. T. & Schroeder, J. Are birds smarter than mathematicians? Pigeons (Columba livia) perform optimally on a version of the Monty Hall Dilemma. Journal of Comparative Psychology 124, 1 (2010).
3.Herbranson, W. T. Pigeons, humans, and the Monty Hall dilemma. Current Directions in Psychological Science 21, 297–301 (2012).
4.Zentall, T. R., Case, J. P. & Collins, T. L. The Monty Hall dilemma with pigeons: No, you choose for me. Learning & behavior 43, 209–216 (2015).
5.Stagner, J. P. & Zentall, T. R. Further investigation of the Monty Hall Dilemma in pigeons and rats. Behavioural processes 112, 14–21 (2015).
6.Gilovich, T., Vallone, R. & Tversky, A. The hot hand in basketball: On the misperception of random sequences. Cognitive psychology 17, 295–314 (1985).
7.Korb, K. B. & Stillwell, M. The story of the hot hand: Powerful myth or powerless critique. in international conference on cognitive science (2003).
8.Miller, J. B. & Sanjurjo, A. Surprised by the gambler’s and hot hand fallacies? A truth in the law of small numbers. (2016).
9.Miller, J. B. & Sanjurjo, A. A cold shower for the hot hand fallacy. (2014).
10.Miller, J. B. & Sanjurjo, A. A Bridge from Monty Hall to the (Anti-) Hot Hand: Restricted Choice, Selection Bias, and Empirical Practice. (2015).
11.Collaboration, O. S. & others. Estimating the reproducibility of psychological science. Science 349, aac4716 (2015).
12.Bargh, J. A., Chen, M. & Burrows, L. Automaticity of social behavior: Direct effects of trait construct and stereotype activation on action. Journal of personality and social psychology 71, 230 (1996).
13.Cohen, J. The Earth Is Round (p < .05). American Psychologist 997–1003 (1993).
14.Meehl, P. E. Theoretical risks and tabular asterisks: Sir Karl, Sir Ronald, and the slow progress of soft psychology. Journal of consulting and clinical Psychology 46, 806 (1978).
15.Greenland, S. et al. Statistical tests, P values, confidence intervals, and power: a guide to misinterpretations. European journal of epidemiology 31, 337–350 (2016).
16.Haller, H. & Krauss, S. Misinterpretations of significance: A problem students share with their teachers. Methods of Psychological Research 7, 1–20 (2002).
17.Gigerenzer, G. Mindless statistics. The Journal of Socio-Economics 33, 587–606 (2004).
18.Wasserstein, R. L. & Lazar, N. A. The ASA’s statement on p-values: context, process, and purpose. (2016).
19.Cumming, G. The new statistics: Why and how. Psychological science 25, 7–29 (2014).
20.Benjamin, D. J., Berger, J. O. & others. Redefine statistical significance. Nature Human Behaviour (2017).
21.Amrhein, V. & Greenland, S. Remove, rather than redefine, statistical significance. Nature Human Behaviour (2017).
22.Lakens, D. et al. Justify Your Alpha: A Response to “Redefine Statistical Significance.” (2017).
23.Gelman, A. & Loken, E. The garden of forking paths: Why multiple comparisons can be a problem, even when there is no “fishing expedition” or “p-hacking” and the research hypothesis was posited ahead of time. Department of Statistics, Columbia University (2013).
24.Petersen, M. B., Sznycer, D., Sell, A., Cosmides, L. & Tooby, J. The ancestral logic of politics: Upper-body strength regulates men’s assertion of self-interest over economic redistribution. Psychological Science 24, 1098–1103 (2013).
25.Gelman, A. The problems with p-values are not just with p-values. The American Statistician, supplemental material to the ASA statement on p-values and statistical significance 10, 1154108 (2016).
26.Young, S. S. & Karr, A. Deming, data and observational studies. Significance 8, 116–120 (2011).
27.Simmons, J. P., Nelson, L. D. & Simonsohn, U. False-positive psychology: Undisclosed flexibility in data collection and analysis allows presenting anything as significant. Psychological science 22, 1359–1366 (2011).
28.Gelman, A., Hill, J. & Yajima, M. Why we (usually) don’t have to worry about multiple comparisons. Journal of Research on Educational Effectiveness 5, 189–211 (2012).
29.Durante, K. M., Rae, A. & Griskevicius, V. The fluctuating female vote: Politics, religion, and the ovulatory cycle. Psychological Science 24, 1007–1016 (2013).
30.Gelman, A. & Carlin, J. Beyond power calculations: Assessing Type S (sign) and Type M (magnitude) errors. Perspectives on Psychological Science 9, 641–651 (2014).
32.Ioannidis, J. P. A., Stanley, T. D. & Doucouliagos, H. The power of bias in economics research. The Economic Journal, forthcoming, SWP, Economics Series 1, (2016).
33.Cohen, J. The statistical power of abnormal-social psychological research: a review. The Journal of Abnormal and Social Psychology 65, 145 (1962).
34.Sedlmeier, P. & Gigerenzer, G. Do studies of statistical power have an effect on the power of studies? Psychological bulletin 105, 309 (1989).
35.Nord, C. L., Valton, V., Wood, J. & Roiser, J. P. Power-up: A Reanalysis of’Power Failure’in Neuroscience Using Mixture Modeling. Journal of Neuroscience 37, 8051–8061 (2017).
36.Tversky, A. & Kahneman, D. Belief in the law of small numbers. Psychological bulletin 76, 105 (1971).
37.Denny, K. Big and tall parents do not have more sons. (2007).
38.Gelman, A. Letter to the editors regarding some papers of Dr. Satoshi Kanazawa. Journal of Theoretical Biology 245, 597–599 (2007).
39.Gelman, A. & Weakliem, D. Of beauty, sex and power: Too little attention has been paid to the statistical challenges in estimating small effects. American Scientist 97, 310–316 (2009).
40.Bennett, C. M., Miller, M. B. & Wolford, G. L. Neural correlates of interspecies perspective taking in the post-mortem Atlantic Salmon: An argument for multiple comparisons correction. Neuroimage 47, S125 (2009).
41.Vul, E., Harris, C., Winkielman, P. & Pashler, H. Puzzlingly high correlations in fMRI studies of emotion, personality, and social cognition. Perspectives on psychological science 4, 274–290 (2009).
42.Kriegeskorte, N., Simmons, W. K., Bellgowan, P. S. F. & Baker, C. I. Circular analysis in systems neuroscience: the dangers of double dipping. Nature neuroscience 12, 535–540 (2009).
43.Jonas, E. & Kording, K. P. Could a neuroscientist understand a microprocessor? PLoS computational biology 13, e1005268 (2017).
44.Gelman, A. Commentary: P values and statistical practice. Epidemiology 24, 69–72 (2013).
45.Gelman, A. The problem with p-values is how they’re used. Ecology. Online: http://www.stat.columbia.edu/gelman/research/unpublished/murtaugh2.pdf (2013).
46.Aad, G. et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Physics Letters B 716, 1–29 (2012).
47.Meehl, P. E. Why summaries of research on psychological theories are often uninterpretable. Psychological reports 66, 195–244 (1990).
48.Meehl, P. E. Theory-testing in psychology and physics: A methodological paradox. Philosophy of science 34, 103–115 (1967).
49.Meehl, P. E. The problem is epistemology, not statistics: Replace significance tests by confidence intervals and quantify accuracy of risky numerical predictions. (1997).
51.Makel, M. C., Plucker, J. A. & Hegarty, B. Replications in psychology research: How often do they really occur? Perspectives on Psychological Science 7, 537–542 (2012).
52.Meehl, P. E. Appraising and amending theories: The strategy of Lakatosian defense and two principles that warrant it. Psychological Inquiry 1, 108–141 (1990).
53.Ioannidis, J. P. A. Why most published research findings are false. PLoS medicine 2, e124 (2005).
54.Siegfried, T. Odds are, it’s wrong: Science fails to face the shortcomings of statistics. Science news 177, 26–29 (2010).
55.Gelman, A. & Fung, K. Freakonomics: What Went Wrong? American Scientist 100, 6 (2012).

发表/查看评论