从贝叶斯视角看多层模型

多层模型

多层模型常被用于处理嵌套数据(即，具有层次结构的数据)，如，从不同的学校中抽取学生样本(第一层为学生，第二层为学校，学生样本嵌套于学校中)，或从不同社区中抽取居民样本等。追踪数据也可被视为多层数据中的一种，其中第一层为不同的测量时间点，第二层为个体。为阐述多层模型的原理，以一个仅包含一个变量的两层模型为例，模型对应公式如下：

$$ Level 1: y_{ij} = \theta_j + e_{ij} \\Level 2: \theta_j = \mu_{\theta} + r_j $$

其中，$y_{ij}$ 代表第 $j$ 个群组中的第 $i$ 个被试在变量 $y$ 上的得分，$θ_j$ 代表第 $j$ 个群组在变量 $y$ 上的均值，$μ_θ$ 代表 $θ_j$ 的均值。$e_{ij}$ 代表个体水平的误差，服从于 $N(0,σ_e^2)$ 的分布，$r_j$ 代表群体水平的误差，服从于 $N(0,σ_θ^2)$ 的分布。

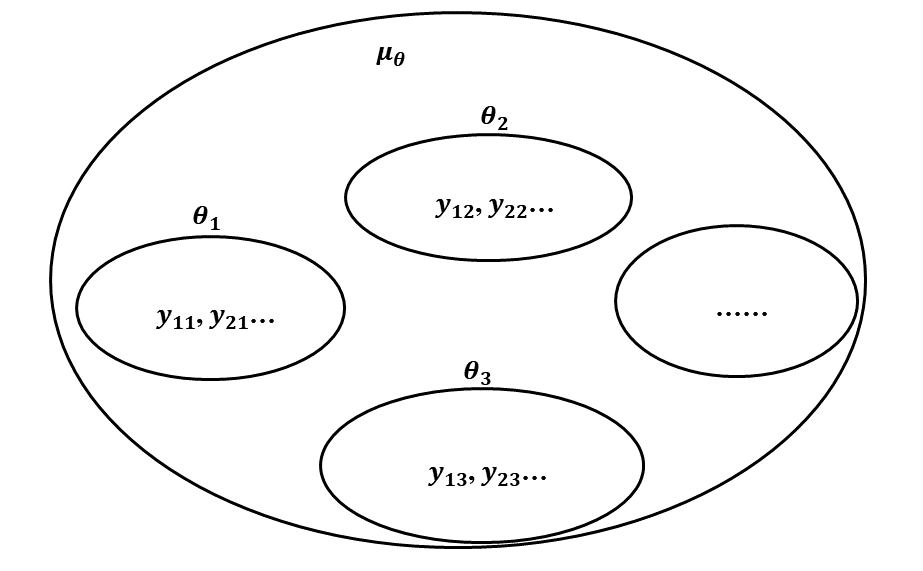
对于这样的数据，如果研究者认为$θ_1=θ_2=⋯=θ_j=μ_θ$，则可以忽略分组变量进行建模，其对应模型如下： $$ y_i=μ+e_i $$ 而如果研究者认为各组之间无法相互提供信息，可以对每组分别建立Level 1 的模型。

多层模型则介于两者之间，认为 $θ_j$ 来源于 $N(μ_θ,σ_θ^2)$ 的正态分布，进而将组间的变异 $σ_θ^2$ (组间差异带来的误差方差)与组内的变异 $σ_e^2$ (个体间差异带来的误差方差)分离开。

贝叶斯思想

多层模型本质上就蕴含着贝叶斯思想，它将参数 $θ_j$ 视为随机变量而非定值 $μ_θ$。而贝叶斯方法和传统频率学派方法本质的区别是：频率学派将未知参数看作常数，根据样本参数估计总体参数；而贝叶斯方法则将未知参数视为随机变量，分析的目的就是得到参数的分布 (王孟成，邓倩文，毕向阳，2017)。

而在贝叶斯多层模型中，不仅将 $θ_j$ 参数视为随机变量，所有参数(如，$μ_θ$ 参数)都会被视为随机变量。研究者对于这些随机变量可以提供一定的先验信息，结合先验信息和数据似然函数，就可以得到参数的后验分布，而通过马尔科夫链蒙特卡洛算法，可以从后验分布中迭代地抽取大量的样本近似地反映后验分布，在该算法达到收敛的前提下，可以利用抽取的样本进行参数估计。

下文将通过实例1展示贝叶斯多层模型结合先验信息的灵活性，并通过实例2演示如何在Mplus软件中进行贝叶斯多层建模。

贝叶斯多层模型

实例1

Jackman(2009)采用了18名棒球运动员在1970年赛季的前45次击球数据预测每个球员在整个赛季中的平均击中率 $θ_j$。 分析采用贝叶斯多层模型，在建模时，研究者对 $θ_j$ 的均值(所有球员的平均击中率 $μ_θ$ )和方差 $σ_θ^2$ 提供了一定的先验分布，研究者指出 $θ_j$ 应当大于0，且基本小于0.4，因为上一次有球员的平均击中率大于0.4已经可以追溯到1941年赛季。研究者进一步猜测平均击中率 $μ_θ$ 主要分布于(0.15, 0.3)之间，基于此，研究者对于 $μ_θ$ 提供了 $N(0.225,(0.15/4)^2)$ 的先验分布，而对于 $σ_θ^2$ 则提供了 $Inv-Gamma(14,0.005)$ 的先验分布以控制 $θ_j$ 主要分布于(0, 0.4)之间，如下图所示。

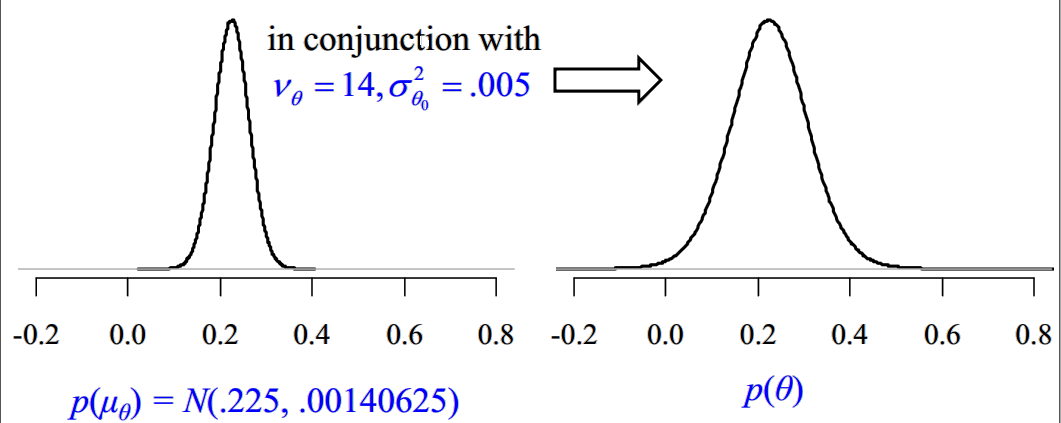
贝叶斯估计结果如下图所示(数据和R代码)：

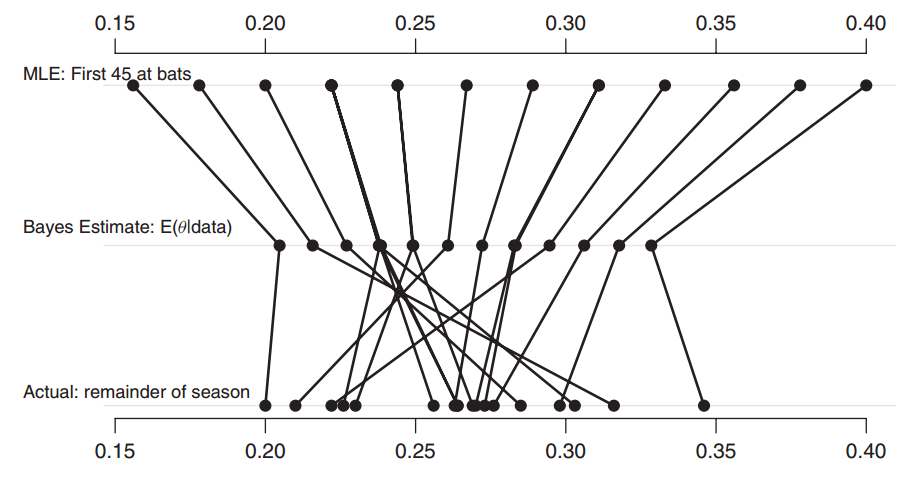
图中第一行MLE的结果指采用极大似然估计对于每个个体分别估计其平均击中率，第二行为贝叶斯估计结果，第三行是球员在整个赛季中真实的平均击中率结果。

相比于分组建模，多层建模将MLE的结果向总体均值 $μ_θ$ 拉近，尽管对于每个个体的击中率产生了有偏估计，但是个体间差异更小，预测误差也更小。

实例2

实例2则以Heck和Thomas(2015)第三章的数据和模型为例，演示如何在Mplus软件中进行贝叶斯多层建模，并灵活地在各个层次间探究变量间的关系。模型如下所示，在组内水平(Within)上，研究者希望探究在控制了性别和种族后，员工对于薪水的满意程度(satpay)对他们的士气(morale)的影响( $β_1$ )，而在组间水平(Between)上，研究者希望探究员工所处部门的整体工资水平(pctbelow)对工作士气的影响，及部门的整体工资水平对个体水平上薪水满意度(satpay)对员工士气(morale)影响的调节作用(即$β_1$是否会随着部门整体工资水平的变化而变化)。

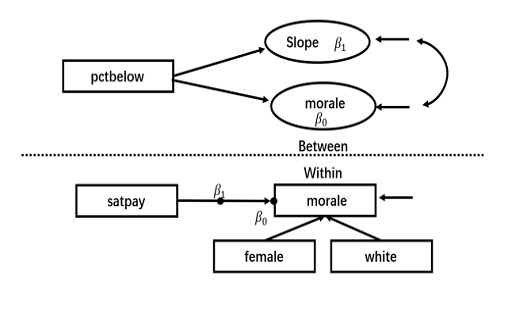
Heck和Thomas(2015)对该模型提供的是极大似然估计，本例中将采用贝叶斯估计，并对参数提供无信息先验分布。Mplus软件默认会对参数提供无信息先验分布，因此代码中无需额外设定。

首先需要将结果变量士气(morale)的方差分解到组内和组间水平(代码和结果)，结果显示，个体间方差为33.312，群体间方差为5.506，计算组内相关系数ICC(Intraclass Correlation)为0.142。ICC指组间方差占总方差的比例，公式如下：

$$ ICC = \sigma_{between}^2 / (\sigma_{between}^2+\sigma_{within}^2) $$

接下来建立假设模型，Mplus代码如下所示，在模型部分，%Between%设定群体水平的模型，%Within%部分设定个体水平的模型。在个体水平部分，用性别、人种和satpay预测morale，并将satpay对morale的效应赋值给S。在群体水平部分，用pctbelow预测morale和S(即检验pctbelow对个体水平上薪水满意度(satpay)对员工士气(morale)影响( $β_1$ )的调节作用)。

模型对应公式如下，其中$\epsilon_{ij}, \mu_{0j} $和$\mu_{1j} $代表误差项:

$$ Level 1: y_{ij} = \beta_{0j} + \beta_{1j} satpay_{ij} + \beta_{2} female_{ij} + \beta_{3} white_{ij} + \epsilon_{ij} \\Level 2: \beta_{0j} = \gamma_{00} + \gamma_{01} pctbelow_j + \mu_{0j} \\ \beta_{1j} = \gamma_{10} + \gamma_{11} pctbelow_j + \mu_{1j} $$

TITLE:	 Model 4: Explaining variation in the level-2 intercept and slope;
DATA:  FILE IS: C:\ Mplus1\ch3new.dat;
	     Format is 5f8.0, 3f8.2;
VARIABLE:	
        Names are deptid morale satpay female white pctbelow lev1wt lev2wt;
        Usevariables are deptid morale satpay female white pctbelow;
        Cluster is deptid;  !分组变量为deptid
        Between = pctbelow; !定义组间变量
        Within = satpay female white; 
Define:	Center satpay female white pctbelow (grandmean);  !中心化处理
ANALYSIS:	
        Type= Twolevel random;   !Twolevel定义两层模型，random定义随机斜率(β1)模型
        Estimator = Bayes;  !定义估计方法
        Biterations = (20000);  !定义模型最小迭代次数为20000次
        Point = Median;  ! 定义点估计报告后验分布的中位数结果
Model:	%Between%
    	morale S on pctbelow;  !用pctbelow预测morale和S
    	S with morale;  !估计morale和S之间的相关
    	%Within%
    	morale on female white;  !用性别和人种预测morale 
    	S | Morale on satpay;  !用satpay预测morale并用S表示satpay对morale的效应，即β1
OUTPUT:	TECH1;
PLOT: TYPE = PLOT2;	!输出各参数的后验分布直方图等

Mplus软件会在算法迭代收敛后输出估计结果，运行过程如下所示

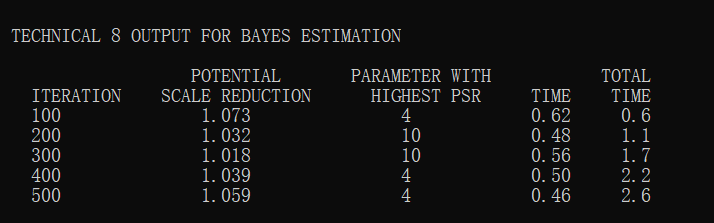
其中，ITERATION代表算法迭代次数，每迭代100次会输出PSR(Potential Scale Reduction)值，当迭代次数大于研究者设定的最小迭代次数且PSR值满足收敛标准后，Mplus软件会停止迭代并输出结果。结果如下所示：

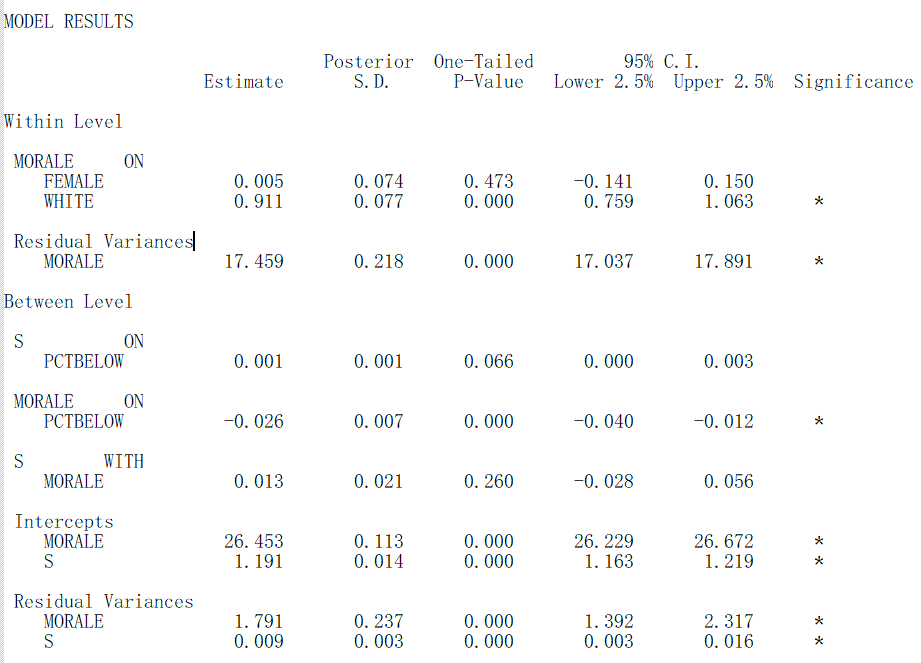
结果显示，员工对于薪水的满意程度将显著的正向预测他们的工作士气($β_1 = 1.196, p < 0.001$)，控制变量性别的效应不显著($𝛽 = 0.005, p = 0.473$)、种族的效应显著($𝛽 = 0.911, p < 0.001$)。所处部门的整体工资水平也能显著预测他们的工作士气($𝛽 = -0.026, p < .001$)，但未发现整体工资水平对薪水满意度和士气的关系间存在调节作用($𝛽 = 0.001, p = 0.066$)。上述无信息先验下贝叶斯方法的估计结果和书中极大似然法的估计结果类似。此时，组内方差被解释了47.6%，残差为17.459，组间方差被解释了67.5%，残差为1.791。

采用R软件中的rjags软件包得到了类似的结果(具体代码和结果)。

总结

多层模型在社会科学等领域的应用非常广泛，尤其是近年来，越来越多的心理学研究开始采用密集追踪研究探究变量间的关系，而多层模型也是处理密集追踪数据的一种常用分析方法。希望本文的介绍可以帮助大家更好地理解多层模型，如果研究者想要深入了解多层模型及其在Mplus软件中的实现方法，也可以参阅Heck和Thomas(2015)一书。

此外，在进行多层数据分析时，实证数据中容易出现第二层样本量不足(如，学校、社区的数目较少)。在这种组数较少的情况下，依赖于大样本渐近理论的频率学方法(如，极大似然估计)容易出现对组间方差的有偏估计，此时采用贝叶斯方法进行模型估计相对更为稳健。而贝叶斯多层模型也可以灵活地结合先验信息(如，以往研究结果或理论)进行参数估计，如果没有准确的先验信息，也可以提供无信息先验分布或模糊信息先验分布。

本例中仅展示了在Mplus软件中提供无信息先验分布进行贝叶斯多层建模的方法，如果研究者需要提供信息先验分布，可以参阅Mplus用户手册(Muthén & Muthén, 1998-2017)。Mplus 8.3也可以被用于分析贝叶斯三层模型，如不同时间点嵌套于个体，个体同时也嵌套于群组的数据。尽管Mplus软件对于一些特殊、复杂的模型难以实现，且能够提供的先验分布的类型也不如Stan和JAGS丰富(如，无法提供双指数先验分布)，但是它易于入门，也基本能够满足大部分研究者的建模需求。

此外，在R软件中也可以采用brms软件包或rjags软件包进行贝叶斯多层建模，它们分别依赖于Stan和JAGS这两个常用的贝叶斯建模软件，实例1、2均给出了采用rjags软件包建模的代码。

参考文献

王孟成, 邓倩文, 毕向阳. (2017). 潜变量建模的贝叶斯方法. 心理科学进展, 25(10), 1682–1695.

Jackman, S. (2009). Bayesian Analysis for the Social Science. John Wiley & Sons, Ltd.

Heck, R. H., & Thomas, S. L. (2015). An Introduction to Multilevel Modeling Techniques: MLM and SEM Approaches Using Mplus. New Jersey: Lawrence Erlbaum Associate Inc.

Muthén, L. K., & Muthén, B. O. (1998-2017). Mplus User’s Guide. Eighth Edition. Los Angeles, CA: Muthén & Muthén.