0.引言
VaR(Value at Risk)是上世纪90年代由JP·Morgan公司在风险矩阵中提出的一种新型风险管理工具,VaR定义简单,计算简便具有很高的实用价值。因此,VaR自诞生以来就在金融领域得到了广泛的应用,且目前在全世界已发展成为金融市场风险测量的主流方法。
1. VaR方法概述
VaR全称为Value at Risk,统译为“在险价值”。其是指:在市场正常波动情况下,在指定的概率水平(置信度)下, 金融资产组合的价值在未来特定持有期T内的最大可能损失,该定义可直观表示为:
$$Prob( \Delta v>VaR_{\alpha})<(1-\alpha) $$
其中,\(\Delta v\)为金融资产组合的价值损失。VaR的严格的数学定义则由Altzner(1999)给出,即
$$VaR_{\alpha}=\inf\{x|Prob(\Delta v\leq x)>1-\alpha\}$$
其中,\(inf{\{x|A}\}\)表示使A成立的所有所组成的集合的下确界,其余符号同上。
目前,典型的VaR的计算方法包括:历史模拟法、蒙特卡洛模拟法、方差-协方差法以近年来广为流行的Coplus方法。其中,历史模拟法和蒙特卡罗模拟法属于全值估计方法,其中历史模拟法的特色在于不需要对市场因子的统计分布进行假设,因此有希望较好地处理金融事件序列中的尖峰和厚尾现象。本文将采用历史模拟法以我国上海黄金期货交易所推出的au0901为研究对象,分析测度au0901的VaR值,最后用Kupiec方法对模型进行有效性检验。
2. 历史模拟法简介
2.1 历史模拟法的定义
历史模拟法是计算VaR的一种非参数方法,通常适用于那些不易取得完整的历史交易资料的金融资产的VaR值的计算。这种方法的核心是用给定历史时期上所观测到的市场因子的变化来表示市场因子的未来变化,也就是说它用历史上金融资产在一定概率水平下所出现的最大损失值作为相应的VaR值。可以形象的说,历史模拟法是一种“以史为鉴”的VaR计算方法。
历史模拟法计算VaR的具体步骤如下:
1、 收集数据资料,确定市场因子。
2、 确定模拟的时间长度N。
3、 对所选取的时间长度N的历史资料计算计算金融资产的收益率。
4、将计算出的收益率按从小到大的顺序进行排序,并按照不同的置信水平计算出相应的分位数,即得到VaR值。
历史模拟法的重点环节是确定合适的历史资料的时间长度N。一般而言,只有足够长的的时间长度,才有可能描述在极端状况下的风险值。如果模拟的时间长度过小,就无法精准刻画金融资产的VaR值。然而,如果模拟的时间长度过长又会因为吸收了过多的历史陈旧信息而是的VaR值的计算不精确。
2.2 历史模拟法的优缺点
1、历史模拟法的优点
(1)不需要对市场因子的统计分布进行假设
历史模拟法完全依赖历史资料进行VaR的计算,不需要对市场因子的统计分布进行假设,可以较精确刻画市场因子的特征,例如一般资产报酬具有的厚尾、偏态现象就可能透过历史模拟法表达出来 。
(2)不需对市场因子的波动性和相关性进行假设
历史模拟法不须对资产收益率的波动性、相关性进行假设,因为历史资料已经反应资产报酬波动性、相关性等的特征,因此免除了估计误差的问题,历史模拟法相较于其它方法,较不受到模型风险的影响。
(3)完全评价法
历史模拟法是一种非参数方法,因此无论资产或投资组合的收益率是否为常态或线性,波动是否随时间而改变,皆可采用历史模拟法来衡量其风险值。
2、 历史模拟法的缺点
应用历史模拟法计算VaR值主要有以下缺点:
(1)历史资料的耗费大量人力物力
历史模拟法一般需要庞大的历史资料库。数据储存、校对、除错等工作都需要庞大的人力与资金来处理,这是一个复杂繁琐的且极易出错的过程。
(2)极端事件的损失不易被模拟
一般而言,重大极端事件的损失比较罕见,所以在进行历史模拟时,很难将极端事件包罗在内,因此采用历史模拟法是常常无法估计出极端事件的发生。
(3)因子的变动假设
历史模拟法假定未来风险因子的变动会与过去表现相同的假设,然而这不一定可以反映现实状况。随着时间的发展,影响金融资产收益的各种因素都在发生这变化,时过境迁之后,未来的市场因子变化可能会异于历史状况,这是历史模拟法最大的软肋。
3. 模型的检验方法
VaR模型的检验方法有很多种,其中Kupiec(1995)提出的失败率检验法最具权威性和实用性。失败率检验法的基本思想是:如果VaR模型计算的VaR 值是准确的,那么金融资产实际损失超过VaR值的例外可视为从一个二项分布中出现的独立事件,即如果损失小于VaR 值,则为一个成功事件(记为1) ,如果损失大于VaR 值,则视为一个失败的事件(记为0)。在原假设 中,P =N/T,其中N 为失败(例外) 天数,即实际损失超过VaR值的天数;1-P为VaR的置信水平; T为实际考察天数。Kupiec 给出了相应的极大似然统计量:
$$LR_{POF}=-2ln[P^N(1-P)^{T-N}]+2ln[(N/T)^N(1-N/T)^{T-N}]$$
在零假设成立的条件下,统计量LR服从自由度为1的分布。如果统计量值超过了临界值,我们则拒绝原假设;否则,则接受原假设。
4. 实证分析
4.1 数据基本描述
本文以交易活跃且具有代表性和国际影响力的上海黄金期货的代号为au0901的黄金期货为例来探讨所选方法的优劣。所用数据为每个交易日的开盘价格连续数据,数据来源于上海期货交易所。考虑到数据的可得性和有效性,au0901的时间跨度定为2008年1月16日至2008年12月31日。在剔除没有交易的交易日后,期铜连续合约的数据个数为252个。为方便处理,本文将期货收益率定义为\(r_t=lnP_t-lnP_{t-1}\)。其中,\(P_t\)为连续期货合约第t日的开盘价格。这里,首先用R软件对样本数据进行基本描述,样本收益率的序列图和收益率的直方图如下:
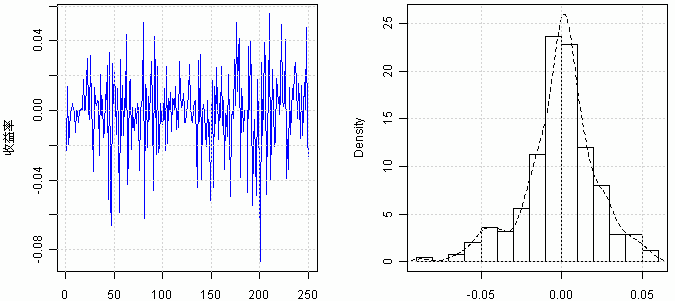
图2 收益率的序列图和收益率的直方图
表1:au0901收益率的基本统计特征
| N | 均值 | 标准差 | 偏度 | 峰度 | J-B值 | D-W值 | Q(25) | Q^2 (25) |
|---|---|---|---|---|---|---|---|---|
| 251 | -0.00072 | 0.0224 | -0.518 | 1.067 | 23.928 | 2.261 | 27.534[0.3] | 47.849[0.03] |
由表1可知,au0901的收益序列是右偏的,且峰度大于正态分布的峰度,从而该序列具有尖峰厚尾的特征,且根据J-B统计量我们可以拒绝原序列为正态分布的原假设。另外,由于D-W统计量的值接近于2,说明该收益序列的自相关性微弱。
4.2 计算及检验VaR
1.用历史模拟法计算VaR值
在应用历史模拟法时,本文选取的历史数据模拟长度为25,置信水平为95%。根据2.2中所述方法计算au0901的时变VaR值,将其与实际收益率对比如下:
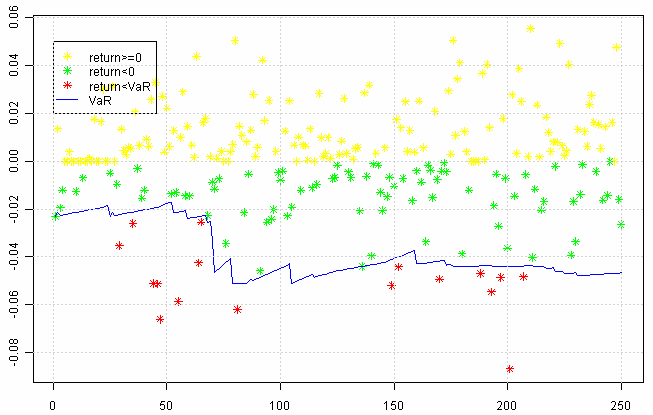
图3 置信水平95%下的时变VaR值与实际收益率对比图
2.Kupiec检验
用前文所述的Kupiec失败率检验方法对模型的结果进行检验,结果如下:
表2:Kupiec失败率检验结果
| 样本长度 | 失败次数 | LR统计量 | 置信水平 | P-value |
|---|---|---|---|---|
| 250 | 16 | 1.54[<3.84] | 95% | 0.215 |
由表2结果可知,在95%置信水平下LR统计量的值小于临界值3.84,因此历史模拟法计算的VaR值通过了Kupiec失败率检验。
4.3 结论
根据前文au0901的VaR的计算结果以及Kupiec的失败率检验结果,我们可以认为:历史模拟法通过了Kupiec失败率检验,可以有效的估计我国黄金期货的风险,适合于我国黄金期货价格的风险度量。
参考文献:
-
王春峰.金融市场风险管理[M].天津大学出版社,2001.
-
张尧庭.金融市场的统计分析[M].桂林:广西师范大学出版社,1998:32-120

发表/查看评论